中3で学習する三平方の定理。直角三角形の辺の長さを求めるときに使う定理ですが、大きい数が出てきたときに計算ミスをした経験はないでしょうか?
この記事では、三平方の定理を使って直角三角形の斜辺でない1辺を求めるときに、 計算をラクにする因数分解のテクニック を紹介します。これをマスターすれば、確実に計算ミスは減りますし、計算スピードもアップしますよ!
三平方の定理をおさらい
三平方の定理は、直角三角形だったら使える定理で次の関係が成り立ちます。
直角三角形の直角をはさむ2辺の長さを \(a\)、\(b\)、斜辺の長さを \(c\) とすると
\(a^2 + b^2 = c^2\)
が成り立つ。
例えば、直角三角形の斜辺と直角をはさむ1つの辺がわかっているとき、もう1つのはさむ辺を求めることができます。
具体例で計算テクニックを使う
下の図のような直角三角形で、\(x\) の値を求めなさい。
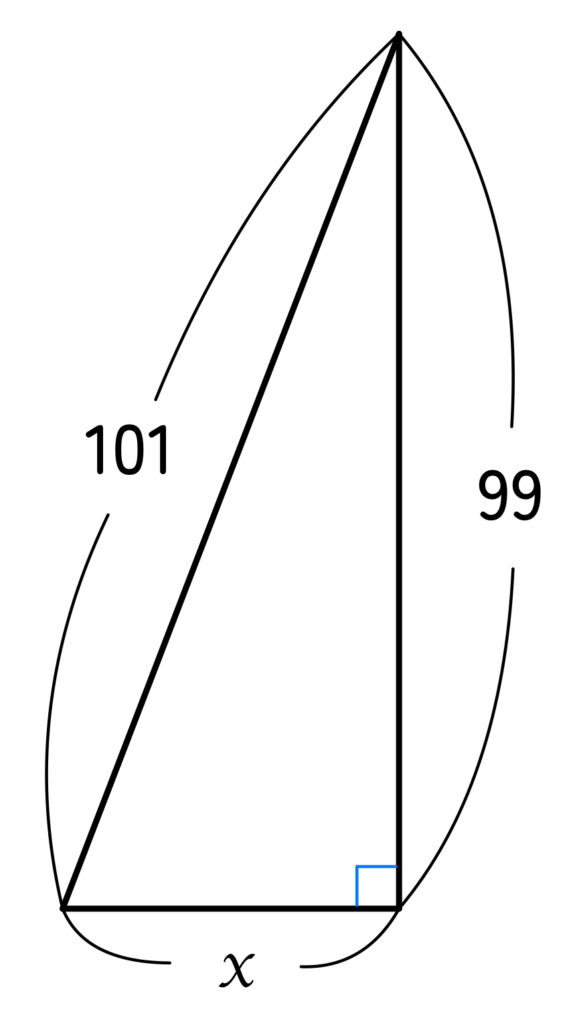
上の図の三角形は直角三角形なので、三平方の定理を使うと次の式が成り立ちます。
\(x^2 + 99^2 = 101^2\)
そして、\(99^2\) を移項して \(x^2\) を求める式に整理します。
\(x^2 = 101^2 – 99^2\)
ここで右辺に注目すると、\(a^2-b^2\) の形になっていますね!
これを因数分解して計算をラクにしましょう。
\(a^2-b^2\) の形は次の公式で因数分解できます。
\(a^2 – b^2 = (a + b)(a – b)\)
これを先ほどの式に適用すると、
\(x^2 = (101 + 99)(101 – 99)\)
右辺を計算して
\(x^2 = 200 \times 2 = 400\)
最後に、平方根を取って \(x\) を求めます。
\(x>0\) より
\(x = \sqrt{400} =\) \(20\)
とわかります。
因数分解を使わない場合との比較
もし因数分解を使わずに直接計算していたら、次のようになります。
\(101^2 = 10201\), \(\quad 99^2 = 9801\) と計算して、
\(x^2 = 10201 – 9801 = 400\) だから
\(x>0\) より
\(x = \sqrt{400} =\) \(20\)
となる。
もちろんこれでも正しい結果が出ますが、大きな数の計算をする必要があり、計算が面倒ですよね。
一方、因数分解 を使うと簡単な計算だけで素早く答えを求めることができます。
頭の中で計算することもできるでしょう。
まとめ
● 三平方の定理の計算で \(a^2-b^2\) の形が出てきたら、因数分解をする!
● 特に、辺の長さの「差が小さい」場合は計算がさらにラクになる!
ぜひこのテクニックを活用して、問題をスムーズに解きましょう!
ガンバレ受験生!
にほんブログ村




コメント