数学者も頭を悩ませた！？モンティ・ホール問題ってなに？

「モンティ・ホール問題」って聞いたことがありますか？
これは一見すると直感に反する、とっても不思議な確率の問題です。でも、ちゃんと考えてみると「なるほど！」と納得できるんです。今回は、この問題とその理由をわかりやすく説明していきます！

モンティ・ホール問題とは？

次のような状況を考えます。

モンティ・ホールが司会のテレビ番組で3つの扉が登場します。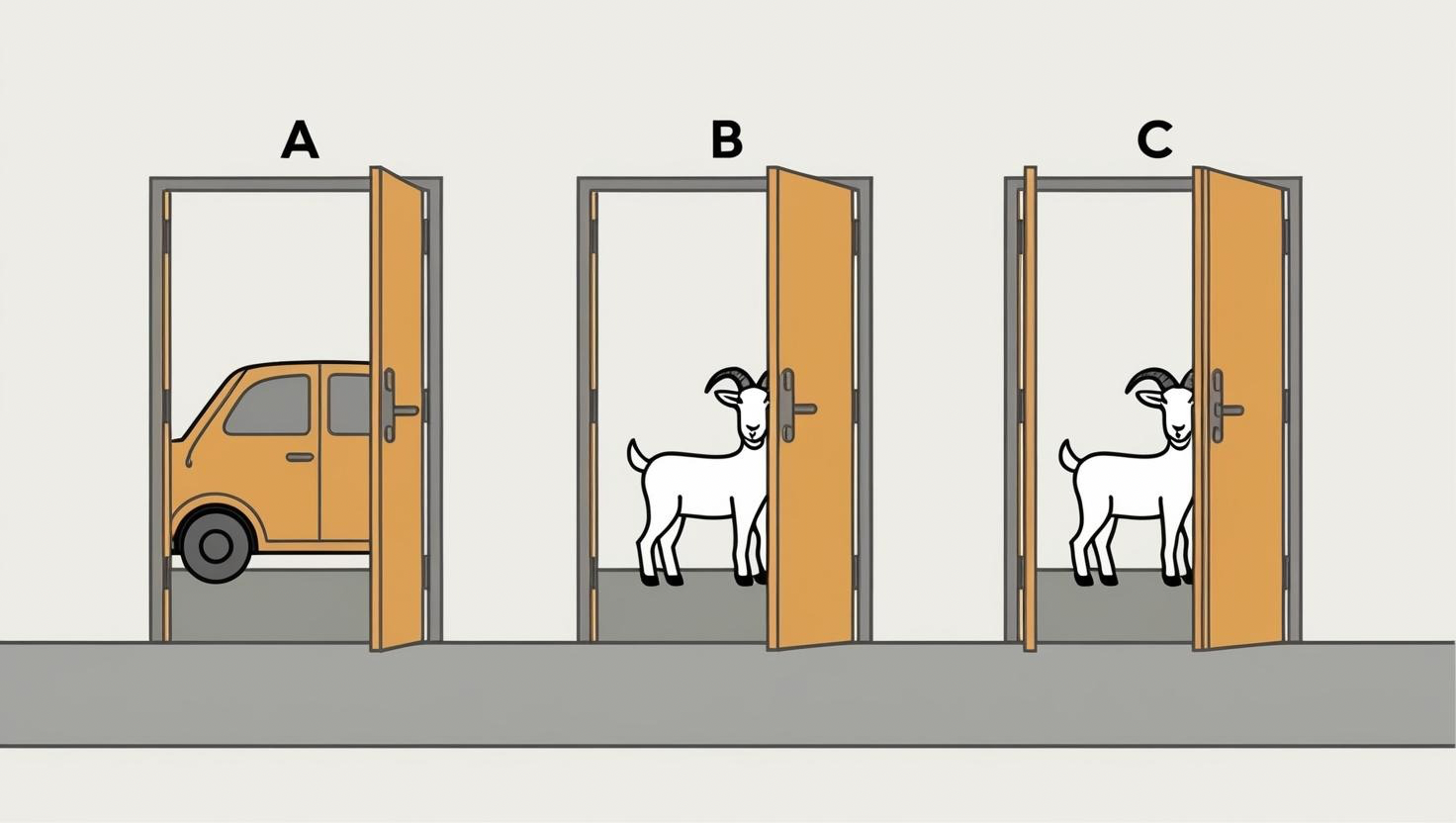

1. 1つの扉には 車（豪華賞品）が隠れています！
2. 残りの2つの扉には ハズレ（ヤギ）が隠れています。
あなたは、この中から1つの扉を選びます。

しかし、そのあと司会者が、 あなたが選ばなかった扉の中からヤギがいる扉を1つ開けます。

すると、残りの扉は あなたが選んだ扉と、もう1つの閉じられた扉の2つ になります。

ここで司会者がこう言います。

さて、あなたは扉を 変えるべき でしょうか？

それとも そのままにする 方がいいのでしょうか？

という問題です。

実は、この問題では扉を 変える 方が勝つ確率が 2倍 になります！

直感的には「どちらを選んでも \(\displaystyle \frac{1}{2}\) じゃないの？」と思うかもしれません。
でも、それは間違いです。

どうして扉を変えると得なのか？

それを説明するために、まず3つの扉の場合を考えます。

最初に選んだ扉の確率は…。

3つの扉の中から1つを選ぶので、車の確率は \(\displaystyle \frac{1}{3}\) です。
残りの2つの扉にはヤギがいるので、ヤギの確率は \(\displaystyle \frac{2}{3}\) です。

そして、司会者は必ずヤギの扉を1つ開けます。このとき、

最初に選んだ扉が車の場合

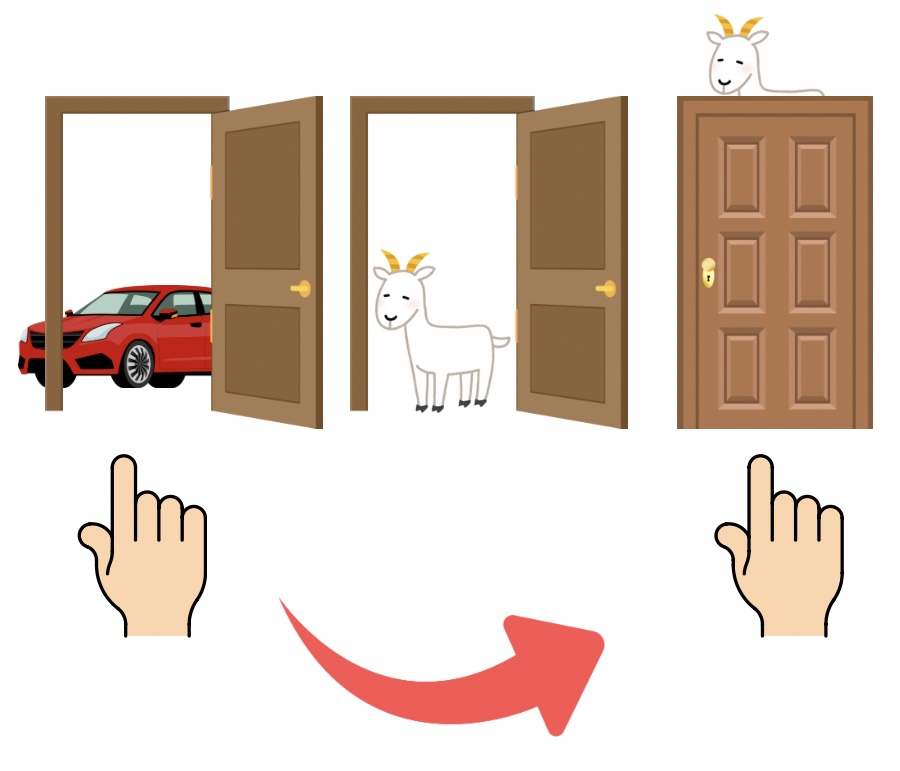
扉を変えると 負け ます（車→ヤギ）。
→ 負ける確率が \(\displaystyle \frac{1}{3}\) ということ。

最初に選んだ扉がヤギの場合

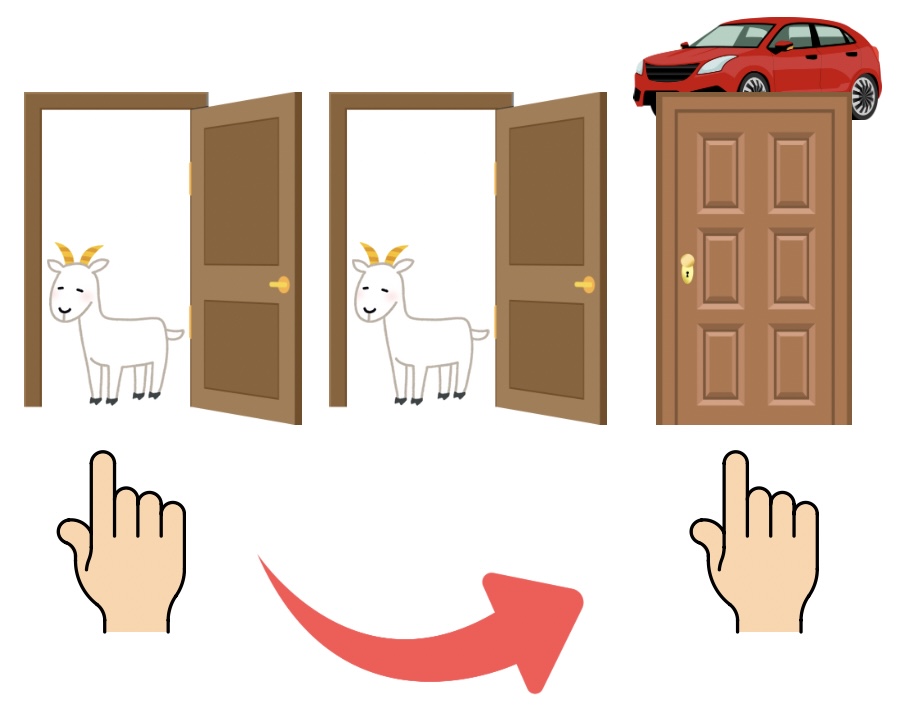
扉を変えると 勝ち ます（ヤギ→車）。
→ 勝つ確率が \(\displaystyle \frac{2}{3}\) ということ。

つまり、扉を変えると 最初にヤギを選ぶ確率 \(\displaystyle \frac{2}{3}\) で車をゲットできるのです！

扉がもっと多い場合を考えてみる

「3つの扉だとわかりにくいなぁ…」と思った人のために、今度は 10個の扉 を考えてみましょう！

このとき、車を選ぶ確率は \(\displaystyle \frac{1}{10}\) しかありません。

つまり、 ヤギを選んでいる確率は \(\displaystyle \frac{9}{10}\) もあります。

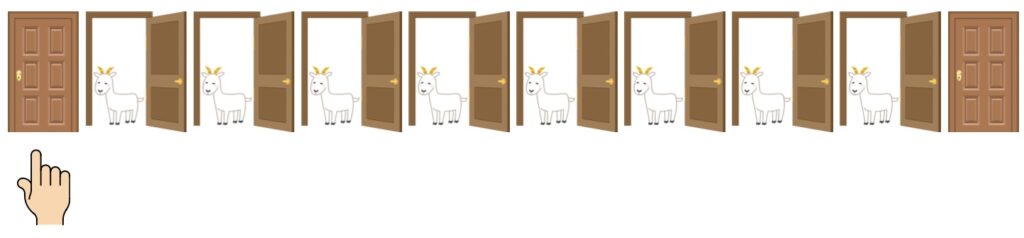
残った扉は、 最初に選んだ扉 と もう1つだけ になります。

ここで考えると、次のことがわかります。

• 最初に選んだ扉が車である確率： \(\displaystyle \frac{1}{10}\)

• 最初に選んだ扉がヤギである確率： \(\displaystyle \frac{9}{10}\)

もし最初にヤギを選んでいた場合（\(\displaystyle \frac{9}{10}\) の確率で起こります）、扉を変えると 確実に車をゲットできます！

つまり、 扉を変えると \(\displaystyle \frac{9}{10}\) の確率で勝ち、そのままにすると \(\displaystyle \frac{1}{10}\) の確率でしか勝てません。

扉が多くなればなるほど、「変えた方が得！」ということがハッキリわかりますよね。

まとめ