ブーメラン型の四角形の角度は？【証明4選】

中2の図形分野の授業やテストで、ブーメラン型の四角形（凹おう四角形という）の角度を求める問題は出ませんでしたか？
この記事では、ブーメラン型の四角形の角度の求め方と、どうしてそうなるかの証明を紹介します！

ブーメラン型の四角形の角度についての性質

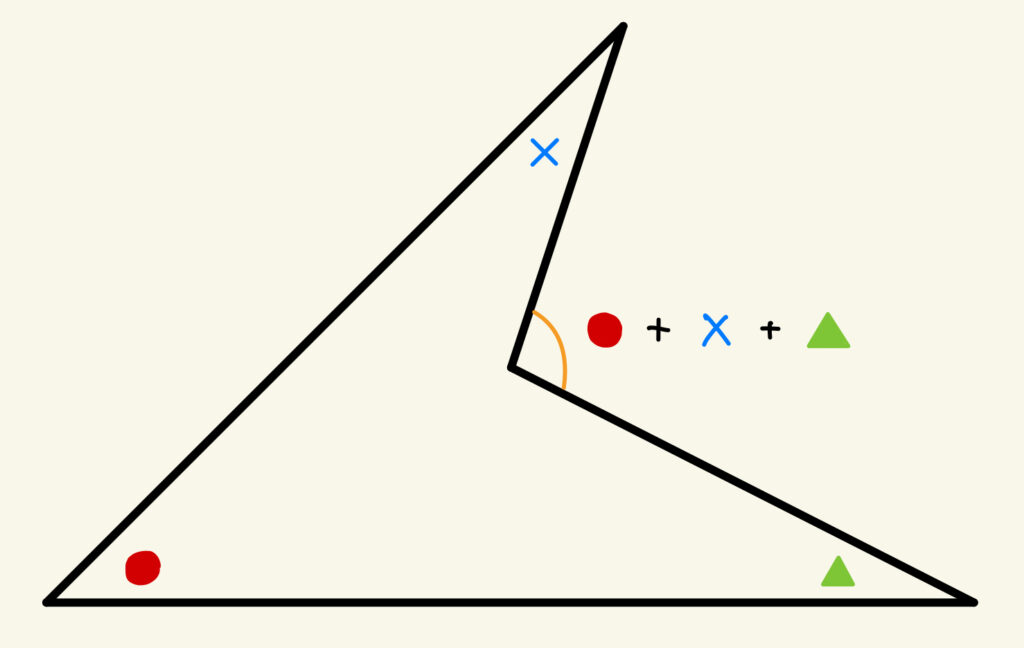
上の図のようなブーメラン型の、凹へこんでいる角の大きさは、
ブーメランの内側の3つの角の和（●＋×＋▲）になります。

以下では、ブーメラン型の角度の性質についての証明を4つご紹介します！

証明その1

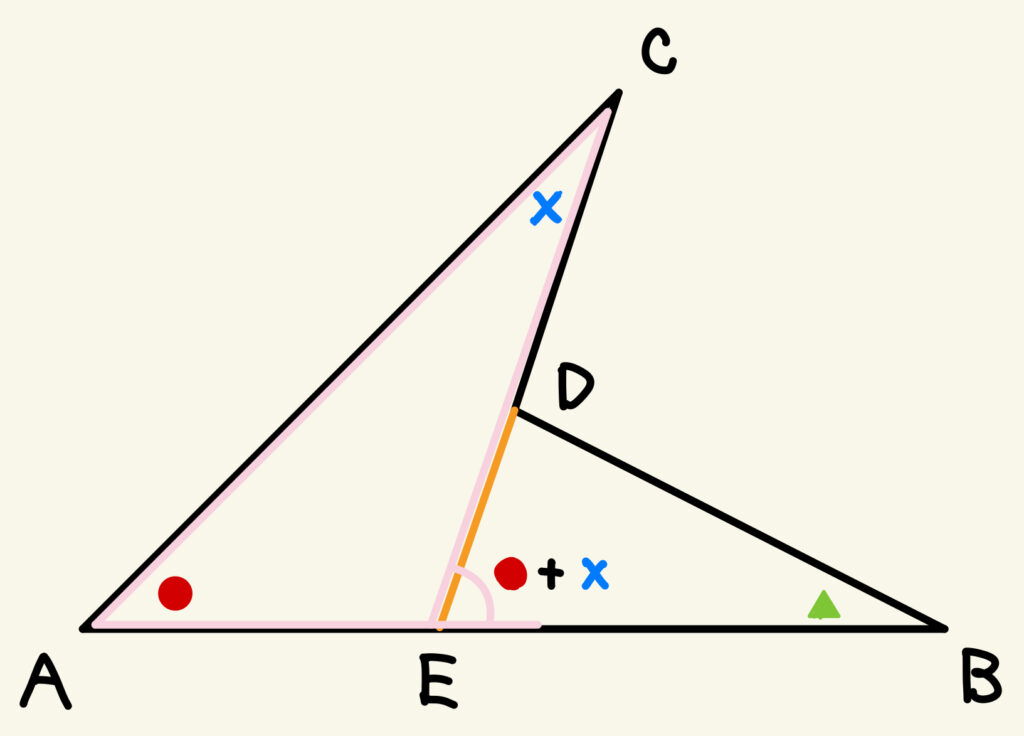
① 辺CDを延長する補助線をひき、辺ABとの交点をEとする。

② △ACEにおいて、頂点Eの外角∠CBEは、外角の性質より●＋×となる。

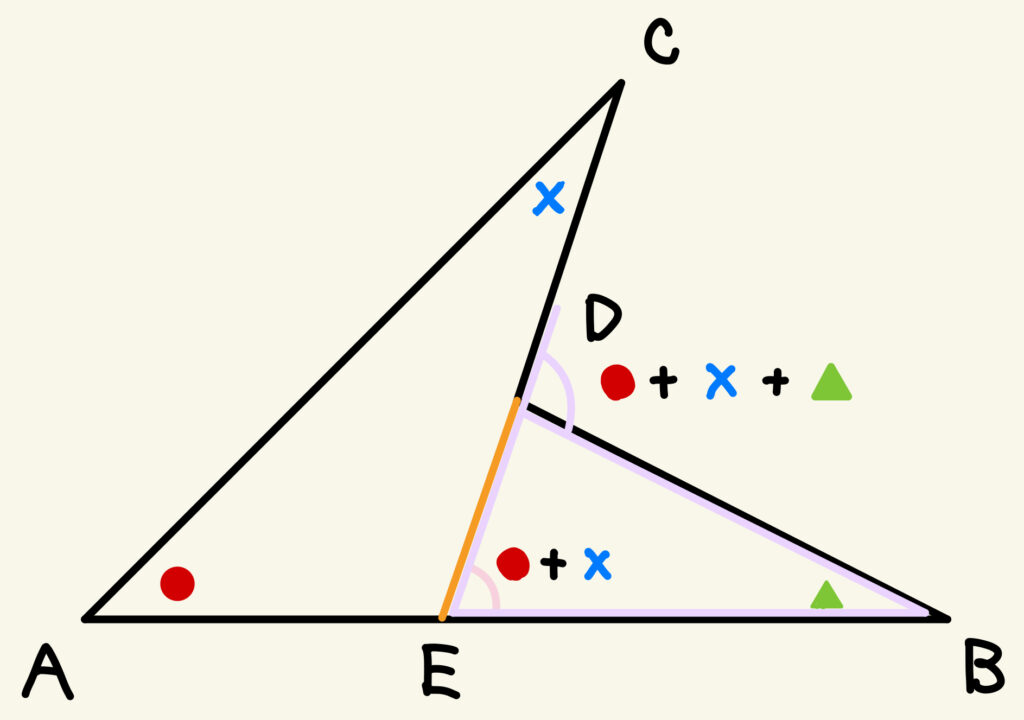
③ △BEDにおいて、頂点Dの外角∠CDBは、外角の性質より●＋×＋▲となる。

証明その2

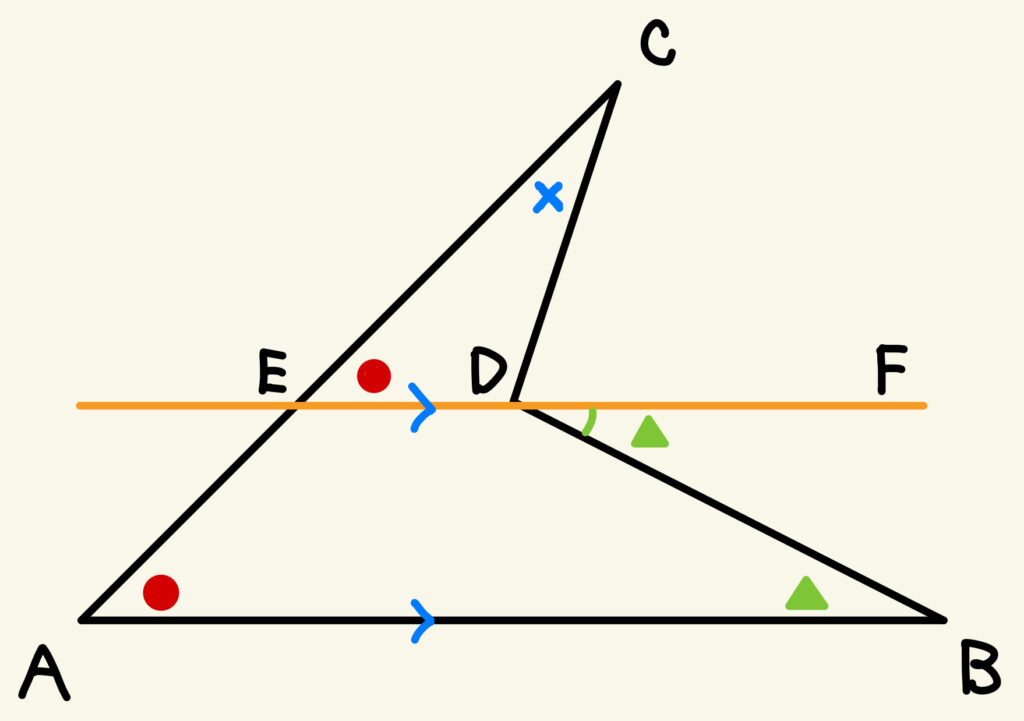
① Dを通る辺ABに平行な補助線をひき、辺ACとの交点をEとし、半直線ED上にFをとる。

② AB//EDより、平行線の同位角は等しいから、∠CED＝●
AB//EDより、平行線の錯角は等しいから、 ∠FDB＝▲

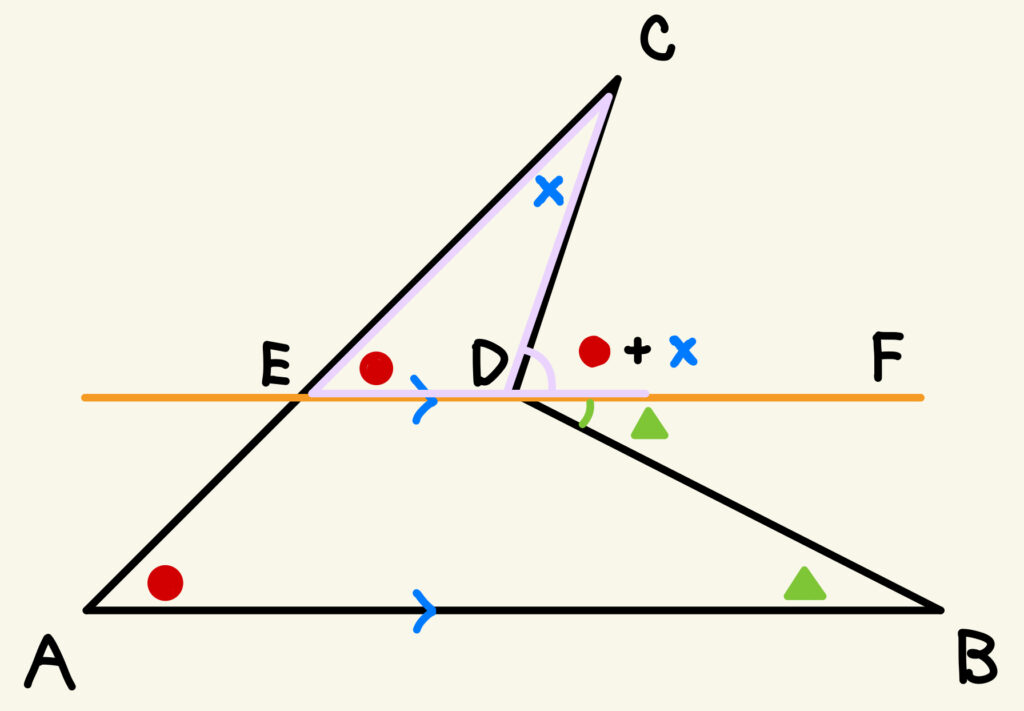
③ △CEDにおいて、頂点Dの外角∠CDFは、外角の性質より●＋×となる。

④ よって、∠CDB＝∠CDF＋∠FDB＝●＋×＋▲となる。

証明その3

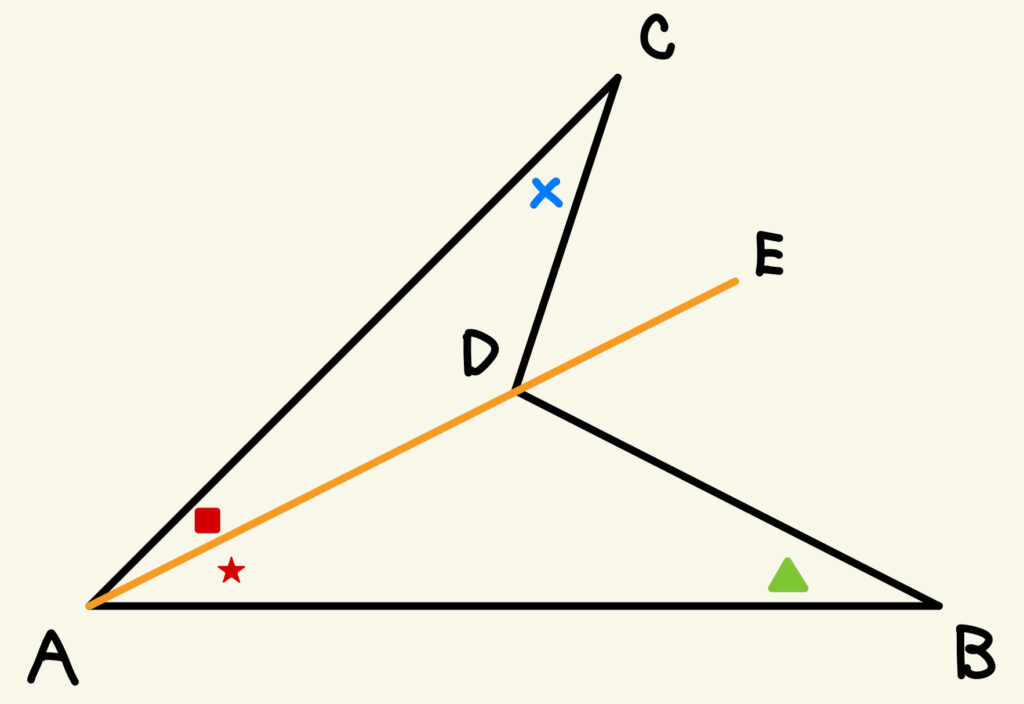
① Dを通る半直線AEとなる補助線をひく。

② ∠CAD＝■、∠BAD＝★とすると（■＝★ではないことに注意！）、■＋★＝● である。

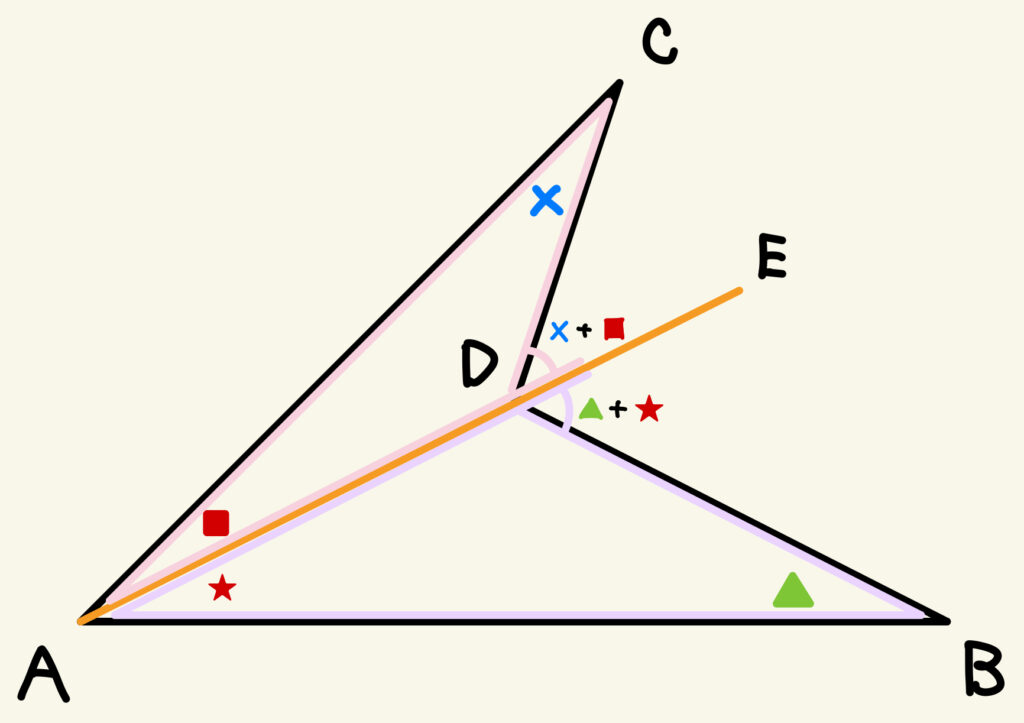
③ △ADCにおいて、頂点Dの外角∠CDEは、外角の性質より×＋■となる。
△ADBにおいて、頂点Dの外角∠BDEは、外角の性質より▲＋★となる。

④ よって、∠CDB＝×＋■＋▲＋★となるが、■＋★＝● であるから、∠CDB＝●＋×＋▲となる。

証明その4

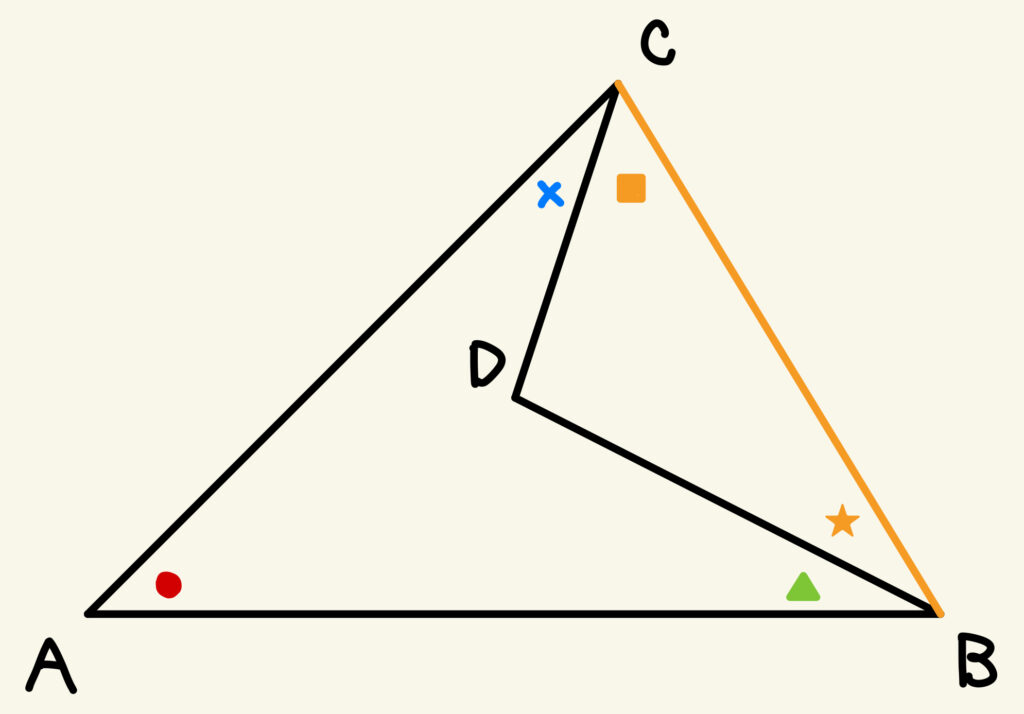
① 頂点CとDを結ぶ補助線をひく。∠DCB＝■、∠DBC＝★とする。

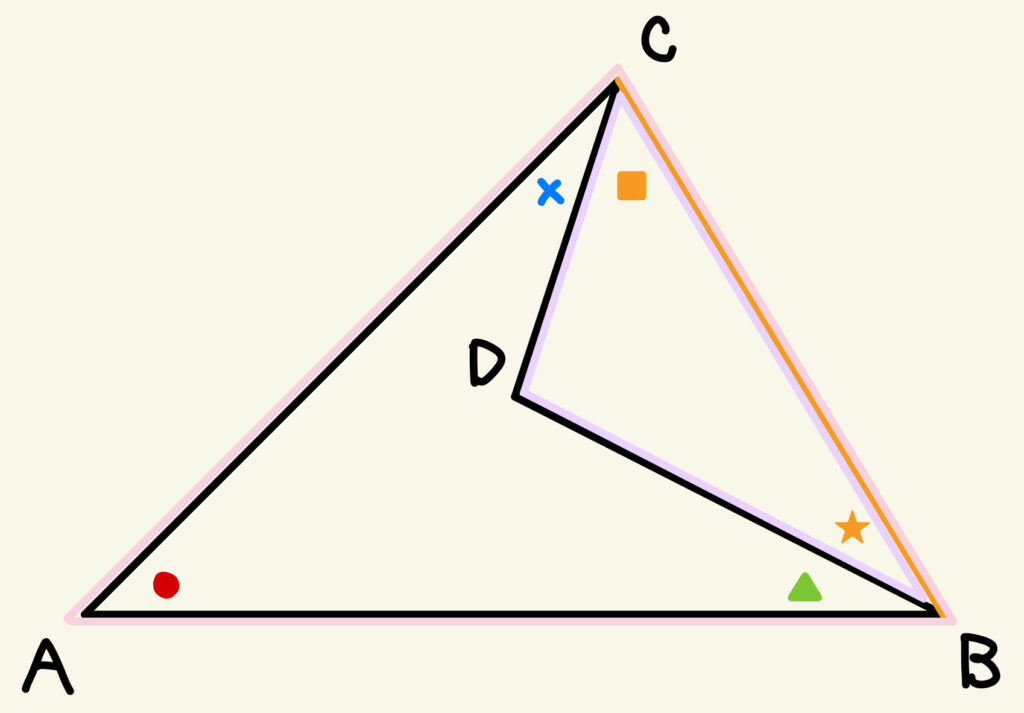
② △ABCにおいて、三角形の内角の和は180°だから、●＋×＋▲＋■＋★＝180° … (i)

③ △CDBにおいて、三角形の内角の和は180°だから、 ∠CDB＋■＋★＝180° … (ii)

④ (i)と(ii)の式を比べて、∠CDB＝●＋×＋▲となる。

まとめ