中学数学では、円周角の定理を用いて図形と角度の関係を学びますが、「円に内接する四角形」もそのひとつです。
この記事では、円に内接する四角形の性質と、実際の問題への活用法について、図とともにわかりやすく解説します!
円に内接する四角形とは?
まずは用語の確認からしましょう。
円に内接する四角形とは、
四角形の4つの頂点がすべて、1つの円周上にあるような四角形
のことです。
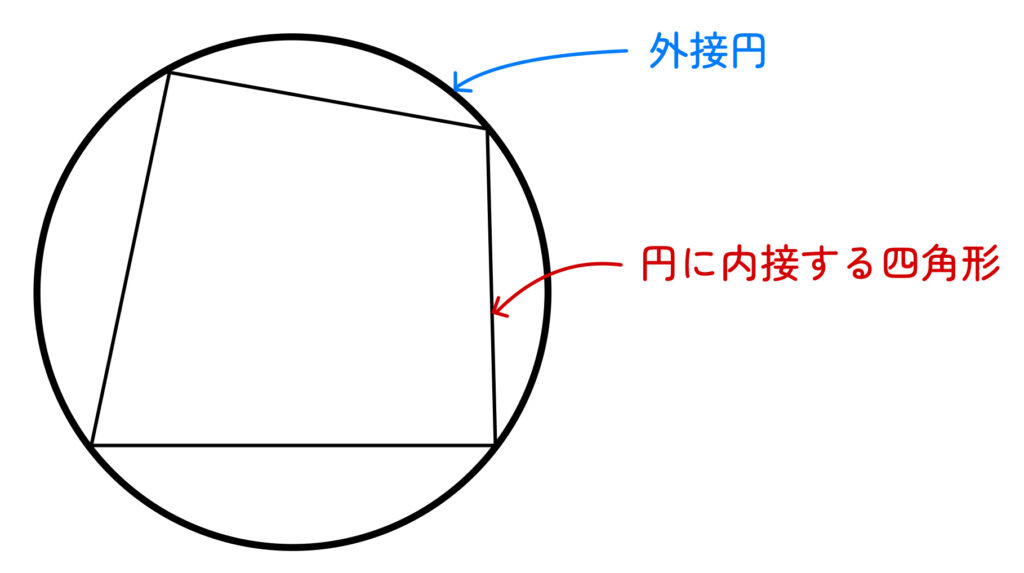
このとき、その円は 四角形の 外接円 と呼ばれます。
円に内接する四角形の性質
円に内接する四角形には、次のような性質があります。
定理
円に内接する四角形において
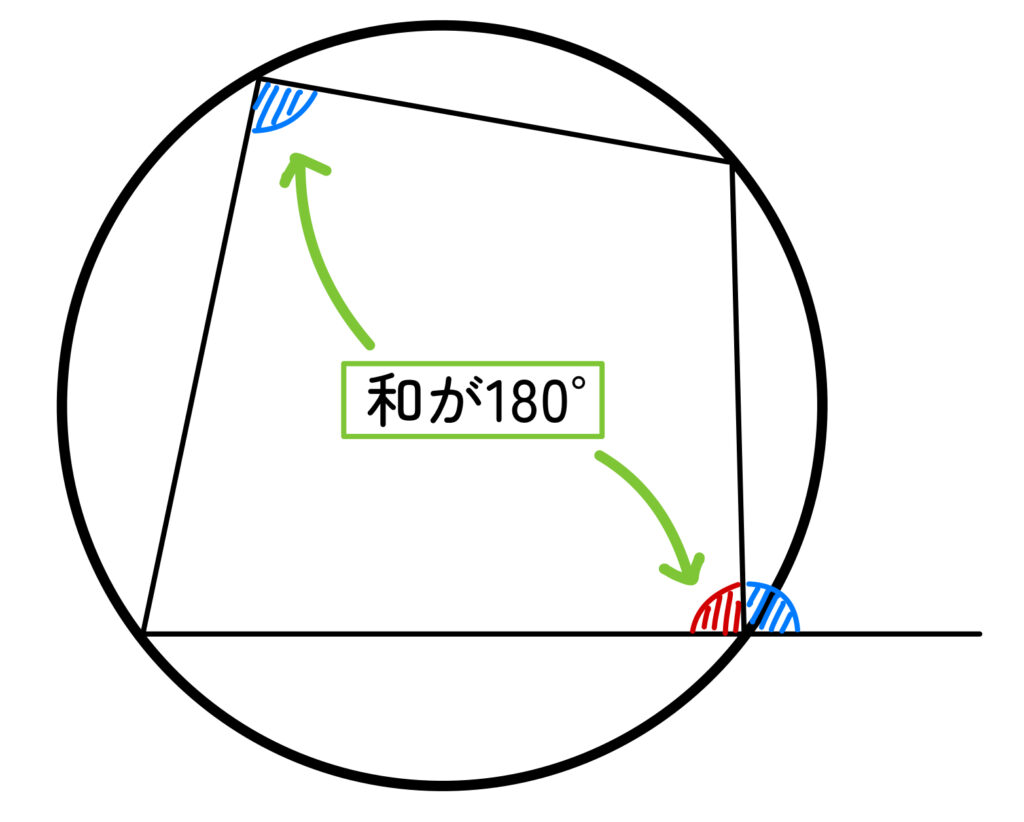
【1】対角の和は180°である。
【2】外角はそれととなり合う内角の対角に等しい。
なぜ定理が成り立つのか?証明しよう!
図をもとに、定理を証明してみましょう。
下の図において、
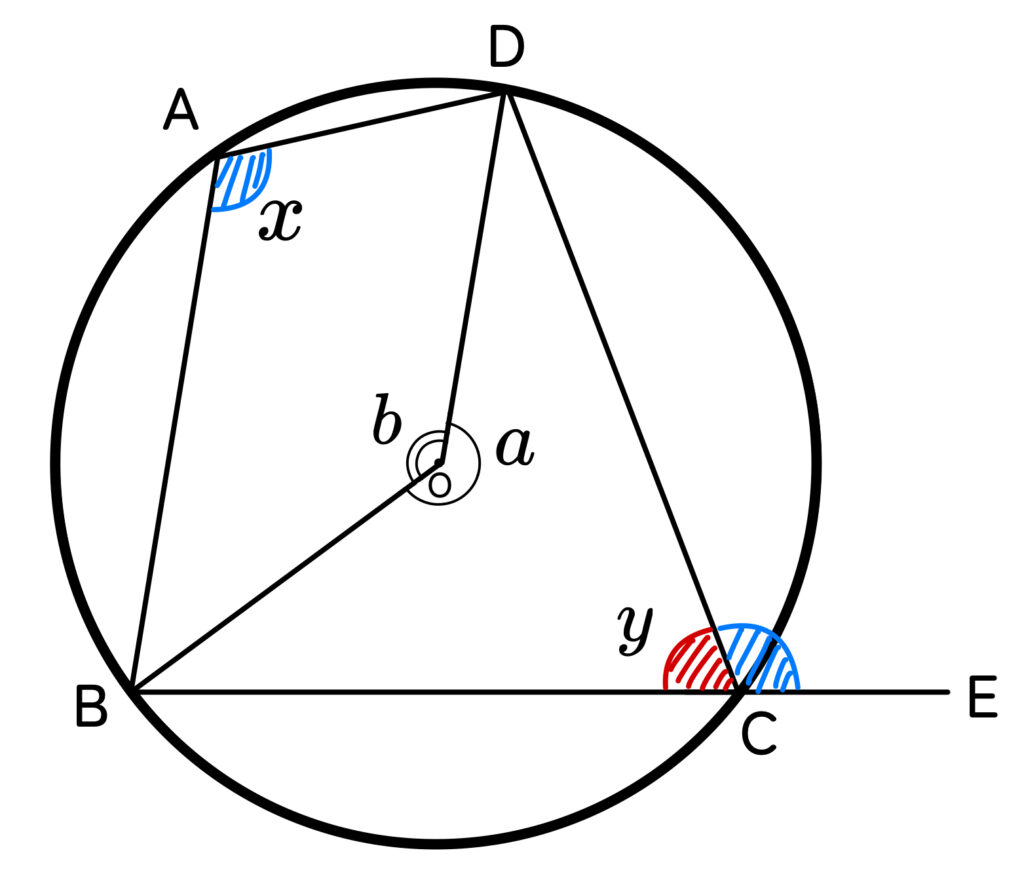
\(∠x+∠y=180°\) と、\(∠DCE=∠x\) であることを示せばよい。
円周角の定理より
\(∠a=2∠x\),\(∠b=2∠y\)
\(∠a+∠b=180°\)
であるから
\(2∠x+2∠y = 360° \)
よって
\(∠x+∠y = 180° \) ・・・ ①
また
\(∠DCE+∠y=180°\) ・・・②
①,②より
\(∠DCE=∠x\)
実際の問題で確認!
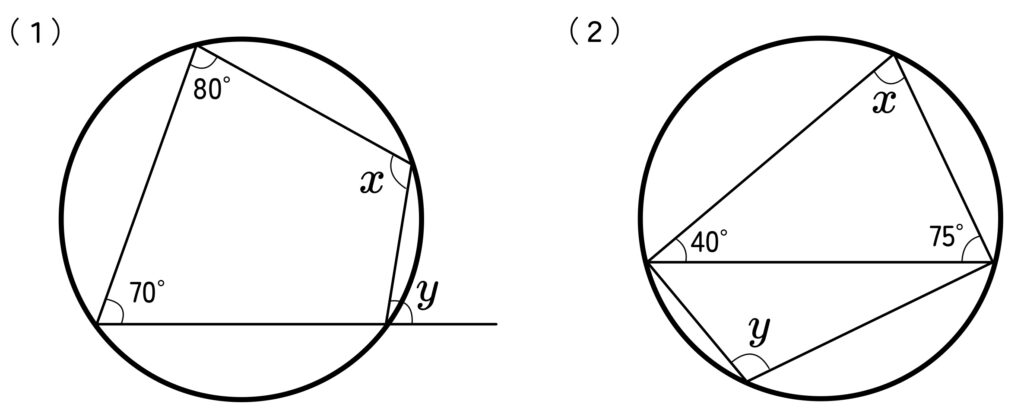
問題
下の図において、\(∠x\),\(∠y\) の大きさを求めなさい。
まとめ
● 円に内接する四角形では、対角の和は180°である。
● 外角はそれととなり合う内角の対角に等しい。
● 実際の問題では、この定理を使えば角度をすばやく求められる!
高校で学習する内容なので、覚えておくと周りの人と差をつけられますよ!
にほんブログ村


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4b5c1fcb.a4bdbaef.4b5c1fcc.e89c80d0/?me_id=1213310&item_id=20138070&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F6417%2F9784860646417.jpg%3F_ex%3D240x240&s=240x240&t=picttext)

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4b5c1fcb.a4bdbaef.4b5c1fcc.e89c80d0/?me_id=1213310&item_id=20210120&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F0326%2F9784761230326.jpg%3F_ex%3D240x240&s=240x240&t=picttext)


コメント