「サイコロを振ったら、1の目が出る確率はどれくらい?」
「ガチャでレアアイテムが出る確率って本当に正しいの?」
こうした疑問は、「確率」という考え方で解決できます。
この記事では、中学校の数学で出てくる「確率」のうち、
・数学的確率
という2つの確率のちがいと関係を、具体例を使ってわかりやすく説明していきます!
そもそも「確率」ってなに?
「確率」とは、あることがらの起こりやすさの程度を数で表したもの です。
たとえば、サイコロを振ったときに「1の目が出る確率」は、
出た目の数(1〜6)のうち、1が出るのは1通りなので、
\(\displaystyle \frac{1}{6}\) = 0.167 (約16.7%)
このように、「どれくらいの割合で起きるのか?」を数字で表したのが確率です。
確率には2つの考え方がある!
中学校で学ぶ確率には、2つの考え方があります。
2.数学的確率
名前が似ているので、ちょっとまぎらわしいかもしれませんが、考え方はぜんぜんちがいます。
統計的確率とは?
✅ 実際にやってみて出た割合
統計的確率は、実験や調査をして出た結果から求める確率です。
たとえば、サイコロを50回投げた結果を見てみましょう。
| 出た目 | 回数 |
| 11 | |
| 5 | |
| 11 | |
| 6 | |
| 5 | |
| 12 |
このとき、「1の目が出た確率」は、
\(\displaystyle \frac{11}{50}\) = 0.22(=22%)
これが「統計的確率」です。実際にやって出た割合なんですね。
✅ 試行回数が増えると、ある値に近づく!
同じサイコロの実験を、もっとたくさん(たとえば1000回)やるとどうなるでしょうか?
投げた結果を見てみましょう。
| 出た目 | 回数 |
| 167 | |
| 166 | |
| 169 | |
| 165 | |
| 166 | |
| 167 |
つまり、「1の目が出る確率」は、
\(\displaystyle \frac{167}{1000}\) = 0.167(=16.7%)
とわかります。
ここでお気づきかと思いますが、1の目以外の目も、出る確率は 0.167くらいになっていますね!
統計的確率は、試行回数が多くなるほど、ある値に近づいていく
という大事な性質があります。
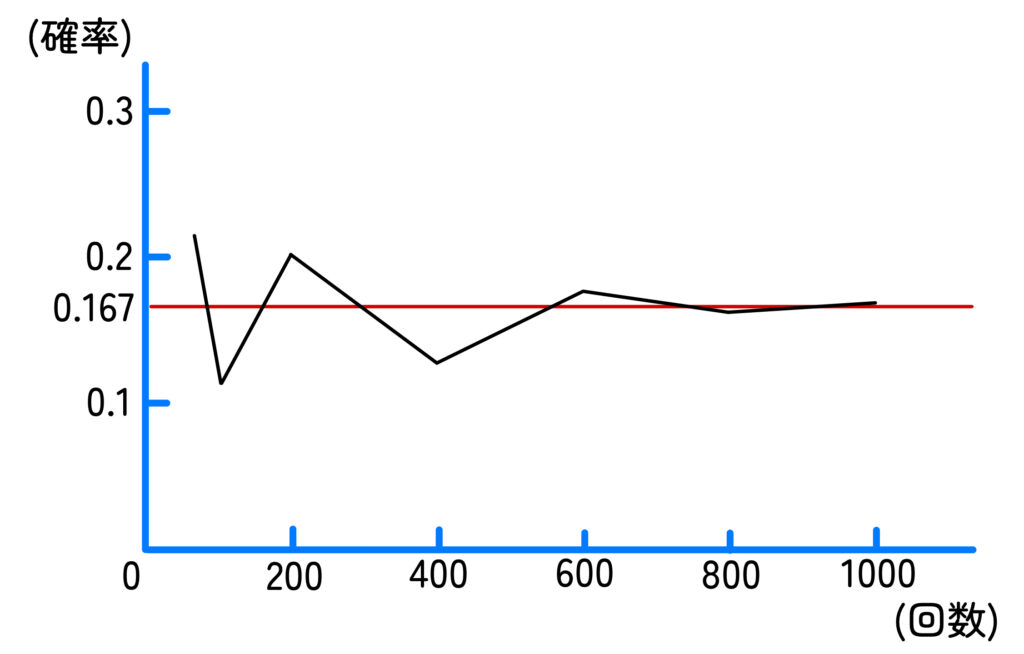
この「近づいていく値」こそが、次に紹介する数学的確率なんです。
数学的確率とは?
一方、数学的確率は、理論的に求めた確率のことです。
先ほどのサイコロのように、1〜6の目が出ることも同じ程度に期待できる(同様に確からしいという)とき、
• 「1が出る確率」も
• 「6が出る確率」も
どれもすべて、
\(\displaystyle \frac{1}{6}\) (あることがらが起こる場合)÷(全ての起こる場合)
と求められます。
これは、実際にやっていなくても、理論だけでわかる確率です。
そして、この \(\displaystyle \frac{1}{6}\) を小数で表すと、 0.167・・・ となり、先ほどの 統計的確率と一致することがわかりますね。
✅ 数学的確率の注意!
ここでちょっとした注意点があります。
たとえば、あるガチャで「レアアイテムが出る確率は5%」と書いてあったとします。
「じゃあ100回引いたら5回は必ず出るんだ!」と思いがちですか、それは間違いです。
確かに「数学的確率」では5%( \(\displaystyle \frac{1}{20}\) )と書いていますが
・100回引いたら、5回出ると“期待される”
・でも実際には4回かもしれないし、6回かもしれない
・運が悪ければ、1回も出ないこともある!
このように、数学的確率=実際の結果そのもの ではないという点に注意が必要です。
まとめ
【統計的確率】
・実際にやってみた結果から求めた確率
・実験の試行回数が多くなるほど数学的確率に近づいていく
【数学的確率】
・同様に確からしいことがらについて、理論的に求めた確率
・「何回やれば何回出る」という保証ではなく、「期待できる程度」を数字で表したものである
にほんブログ村




コメント