【相似な図形】アポロチョコの「いちご」と「チョコ」はどちらが多い？

みなさん１度は食べたことのあるアポロチョコレート。
そのアポロチョコの「いちご」と「チョコ」の部分、どちらが多いのか考えたことはありませんか？

見た目では「いちごの層の方が厚そう」に見えますが、実は数学的に調べると意外な結果になります。今回は、アポロチョコを「円錐」とみなして、相似比・体積比の考え方で比較してみましょう。

アポロチョコの形を考える

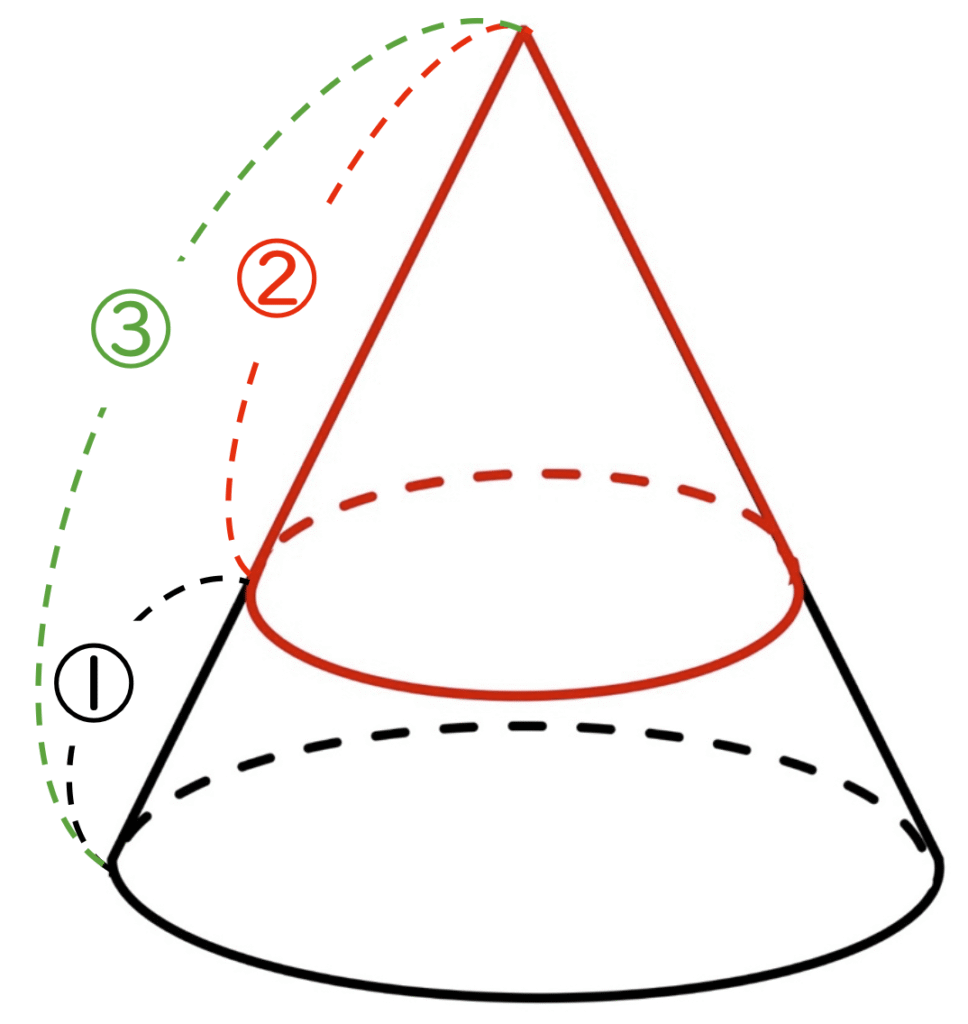
実際のアポロチョコは側面がギザギザしていますが、ここでは「円錐」とみなして考えることにします。

また、いちごの層とチョコの層の比は２：１だと考えます。

つまり、全体の比は“３”ということになります。

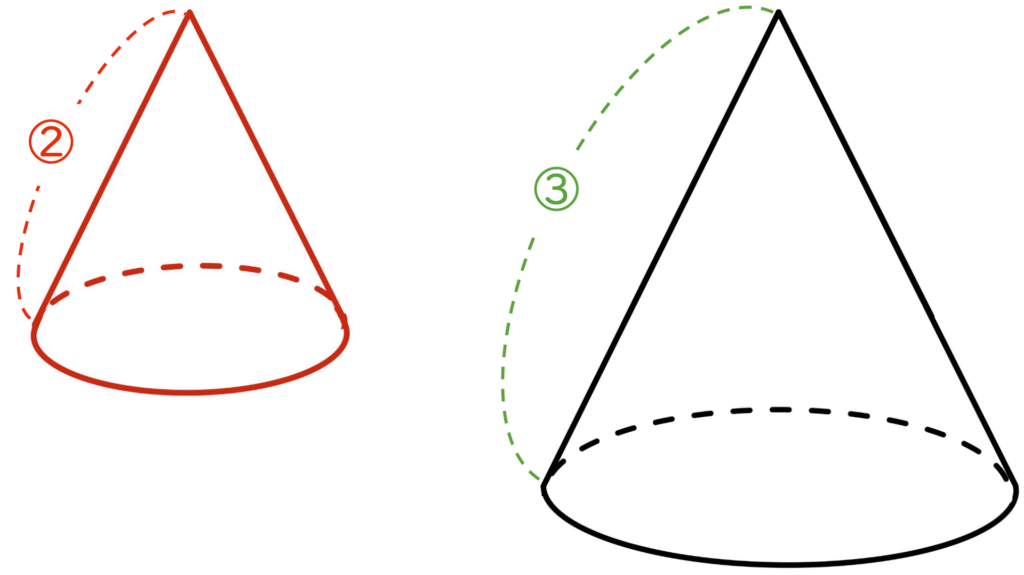
ここで使う考え方は、相似比から体積比を求めることです。

アポロチョコの「いちごの部分の円錐」と「全体の円錐」は相似であり、その相似比は２：３とわかります。

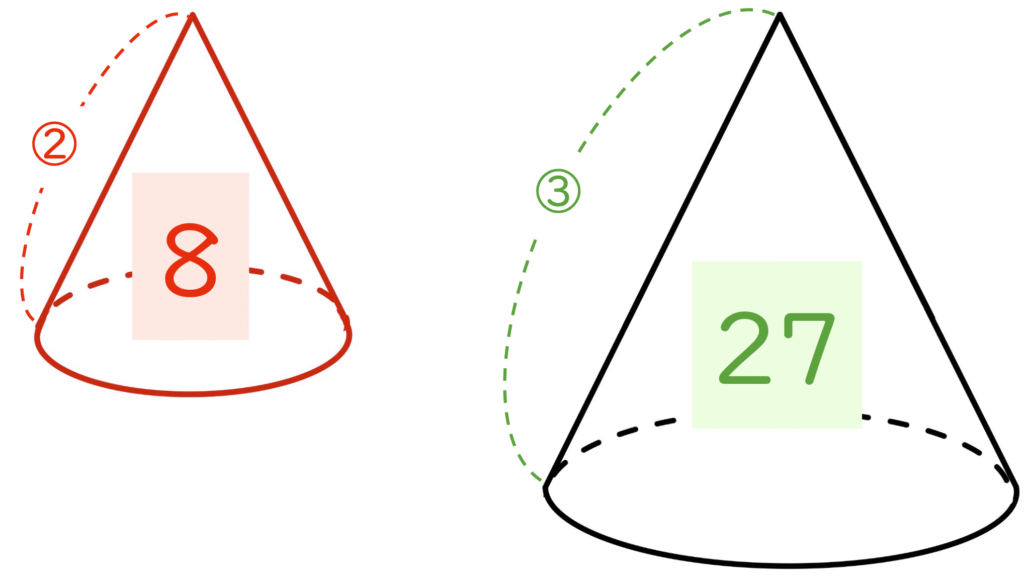
なので、体積比は相似比の３乗 より
（いちごの体積）：（全体の体積）＝８：２７
となります。

よって、（チョコの体積の比）＝（全体）ー（いちご）＝２７ー８＝１９なので

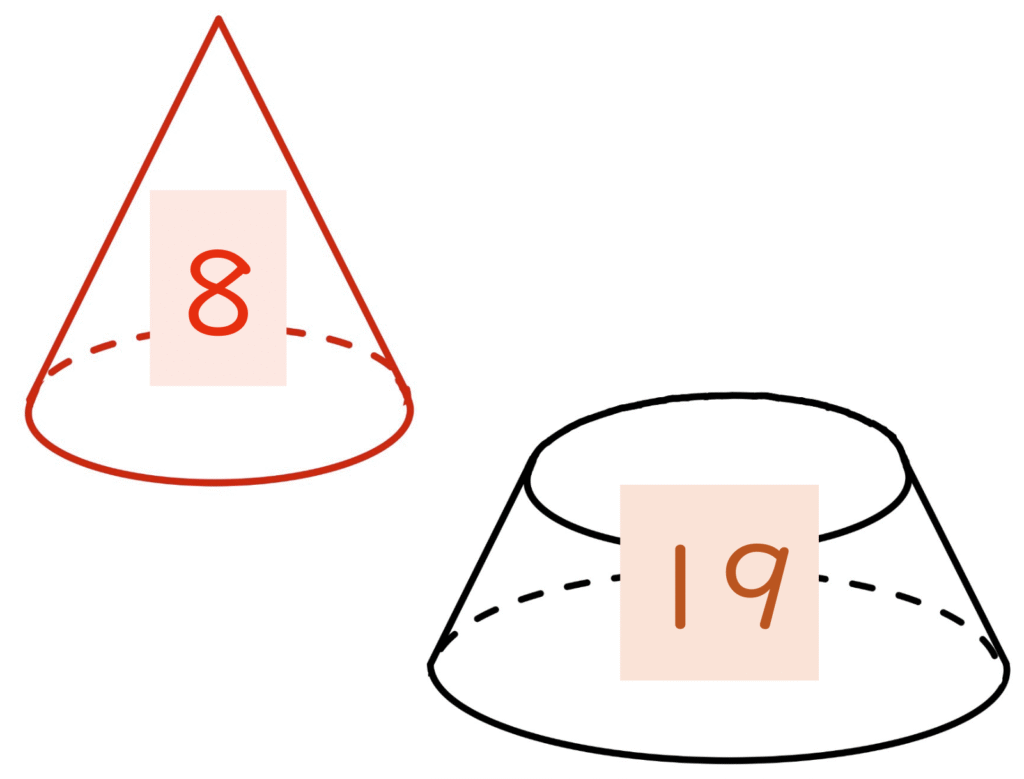
（いちごの体積）：（チョコの体積）＝８：１９

とわかります。

いちごの層の厚さはチョコの層の厚さの２倍なのに、いちごの体積よりチョコの体積の方が多いということですね。

では、チョコの体積はいちごの体積の何倍なのでしょうか。

（いちごの体積）：（チョコの体積）＝８：１９より

「チョコ」は「いちご」の　１９÷８＝ ２．３７５（倍）

ということがわかります。

２倍以上も「チョコの体積」の方が多いのです。

見た目と実際の体積が大きく違う、ちょっと面白い数学の話でした。

身近なお菓子でも、数学の視点で見ると新しい発見がありますね。