1次関数のグラフって、切片が整数ならかきやすいけど、分数だと「え、どこに点をとればいいの?」と迷ってしまうことはありませんか?
この記事では、1次関数のグラフのかき方を徹底解説します!
まずは整数の切片でのグラフのかき方を確認!
次の1次関数のグラフをかきなさい。
\(y=2x+1\)
これは切片が「1」なので、(0,1)のところに点をとります。
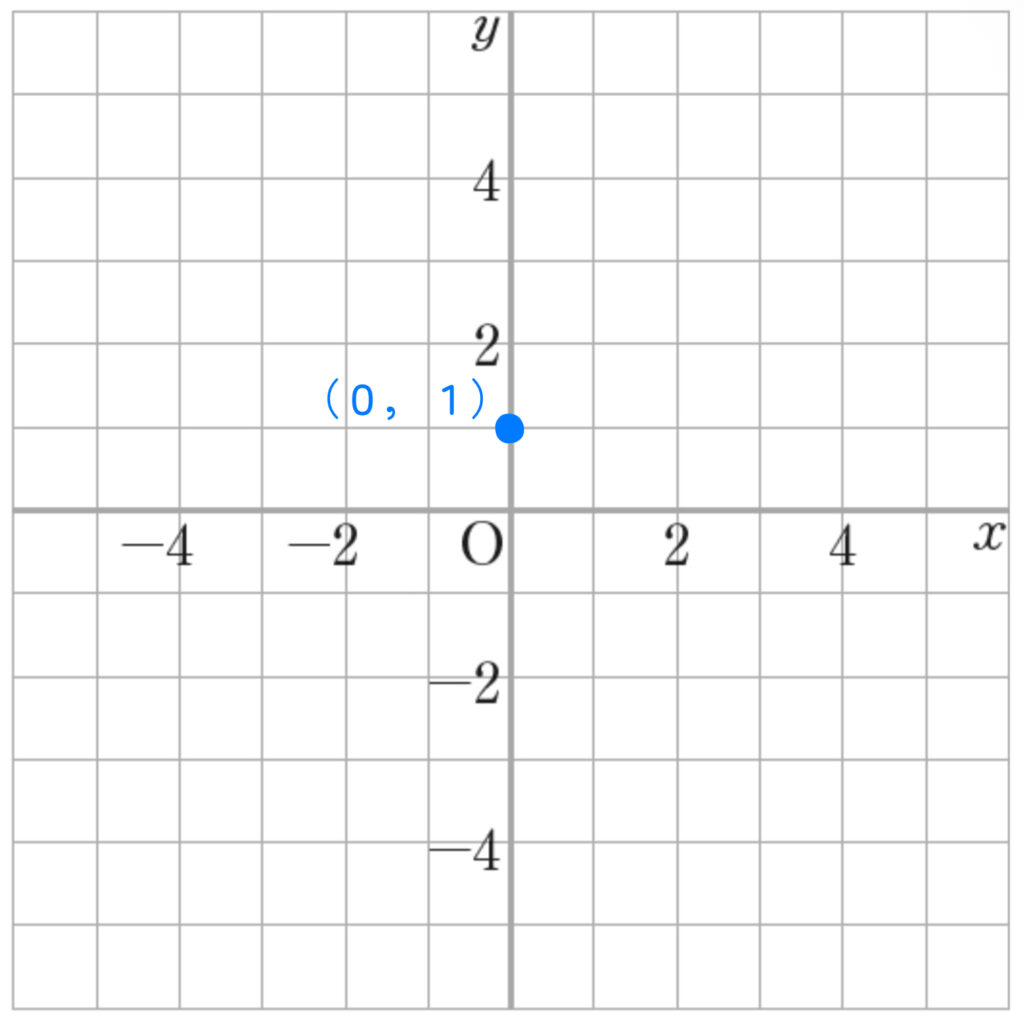
次に、傾きが「2 \(= \displaystyle \frac{2}{1}\) 」だから、「右に1、上に2」動いたところにも点をとって、2点を結べばグラフが完成します!
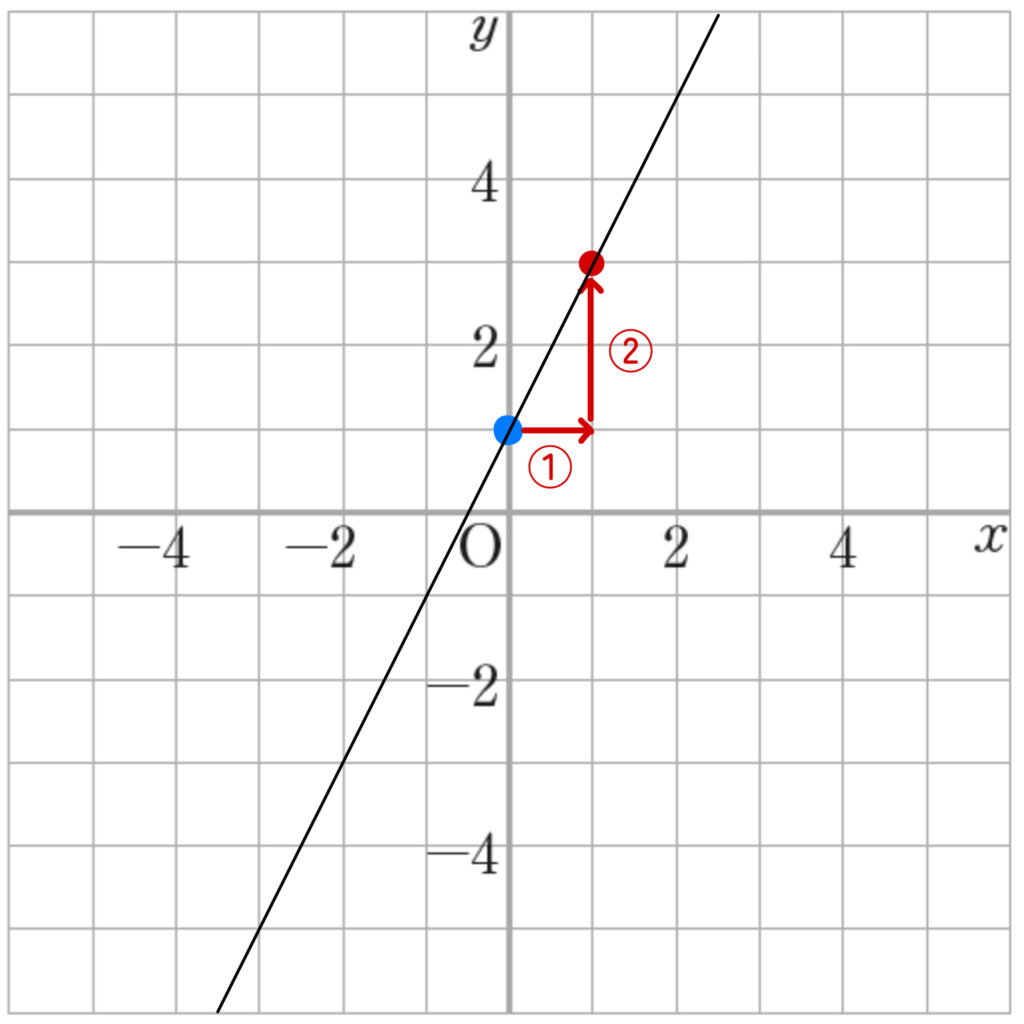
このように、切片と傾きがわかれば、グラフがかけます。
分数の切片だと、どのようにかけばいい?
次の1次関数のグラフをかきなさい。
\(y=\displaystyle \frac{1}{3}x+\displaystyle \frac{4}{3}\)
切片が \(\displaystyle \frac{4}{3}\) …つまり1と3分の1。
\(y\) 軸にそんな中途半端なところ、正確に点をとるのは難しいですよね。
そんなときの解決法はこれ!
\(x\) に整数を代入して、\(y\) も整数になるような点を見つける!
\(x\) に整数を代入する!
\(y=\displaystyle \frac{1}{3}x+\displaystyle \frac{4}{3}\)に、
\(x = 1\) を代入すると
\(y = \displaystyle \frac{1}{3} \times 1 + \displaystyle \frac{4}{3} = \displaystyle \frac{5}{3}\)
つまり、(\(1\) ,\(\displaystyle \frac{5}{3}\) )に点をとればよいですが…
これも中途半端な点ですね。
では、 \(x = 2\) と代入すると?
\(y = \displaystyle \frac{1}{3} \times 2 + \displaystyle \frac{4}{3} = \displaystyle \frac{6}{3} = 2 \)
おっ、\(y\) が整数になりました!
つまり、(\(2\),\(2\)) の点を通るということです!
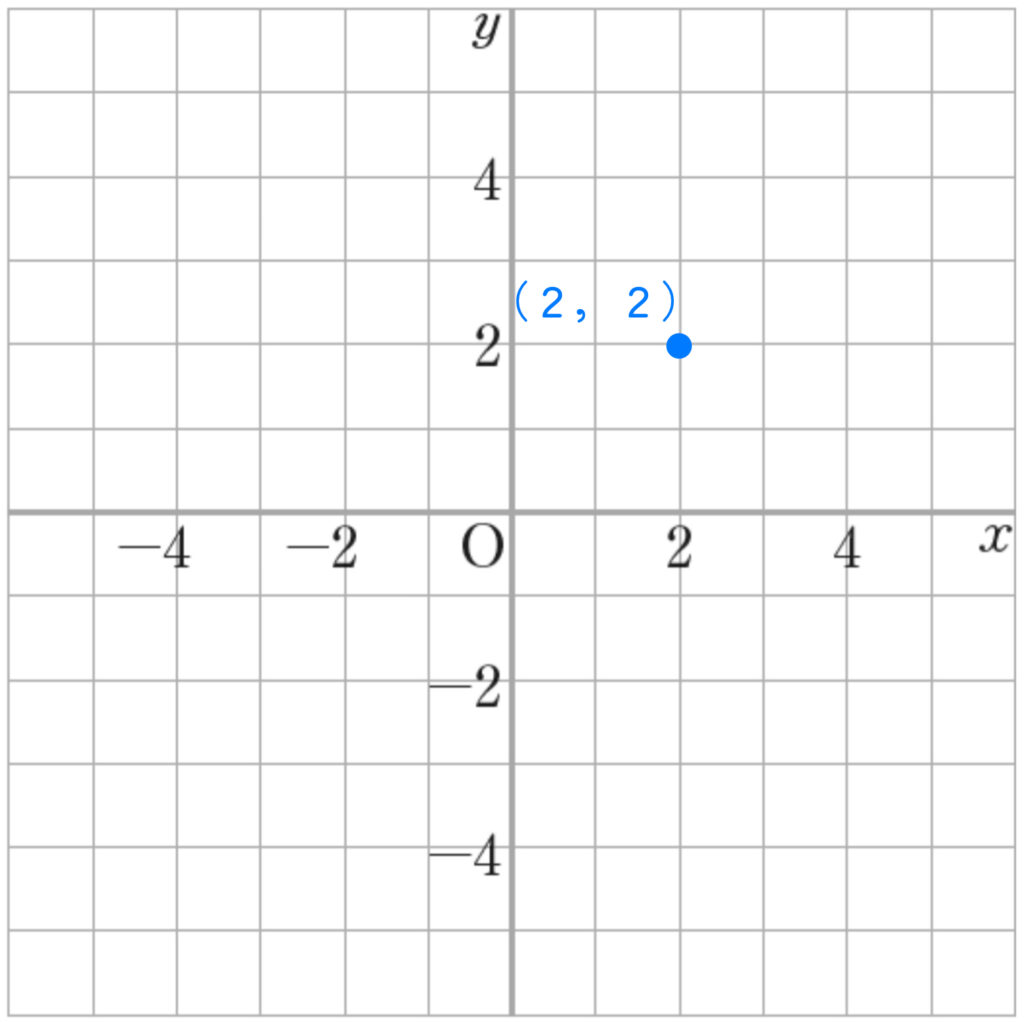
傾きを使って、さらに点をとろう!
\(y=\displaystyle \frac{1}{3}x+\displaystyle \frac{4}{3}\) の傾きは \(\displaystyle \frac{1}{3}\) 。
これは「右に3、上に1」と読むことができます。
さきほど点をとった (2, 2) から、右に3、上に1 動くと…
→ (5, 3) にたどり着きます。
なので、この2つの点
(2,2)と(5,3)
を通る直線が、\(y=\displaystyle \frac{1}{3}x+\displaystyle \frac{4}{3}\) のグラフになります!
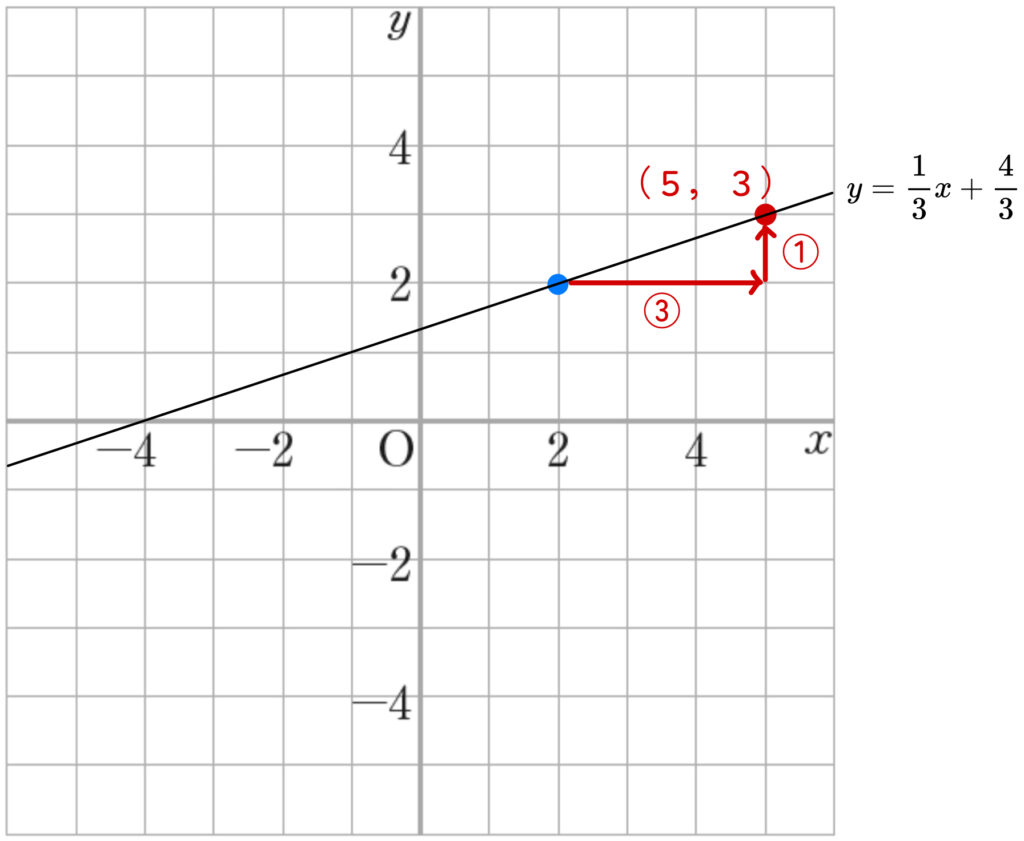
まとめ
1次関数で、分数の切片のグラフは
① 1次関数の式の \(x\) に整数を代入して、\(y\) も整数になるような点を見つける!
② 見つけた点から、傾きを使って2点目をとる!
③ 2つの点を結べばグラフが完成!
この方法で、1次関数のどんなグラフでもかけるようになります!
にほんブログ村




コメント