同側内角とは？和は180°になるのか？【証明】

中2の図形分野で学習する内容として、2つの角の位置関係を表す対頂角・同位角・錯角があったと思います。実はそれ以外に、「同側内角」という位置関係があるのです。
また、同側内角の和は平行線のときに180°になるのです。
この記事では、同側内角の意味、平行線のときに和が180°になる理由を紹介します！

「同側内角」とは

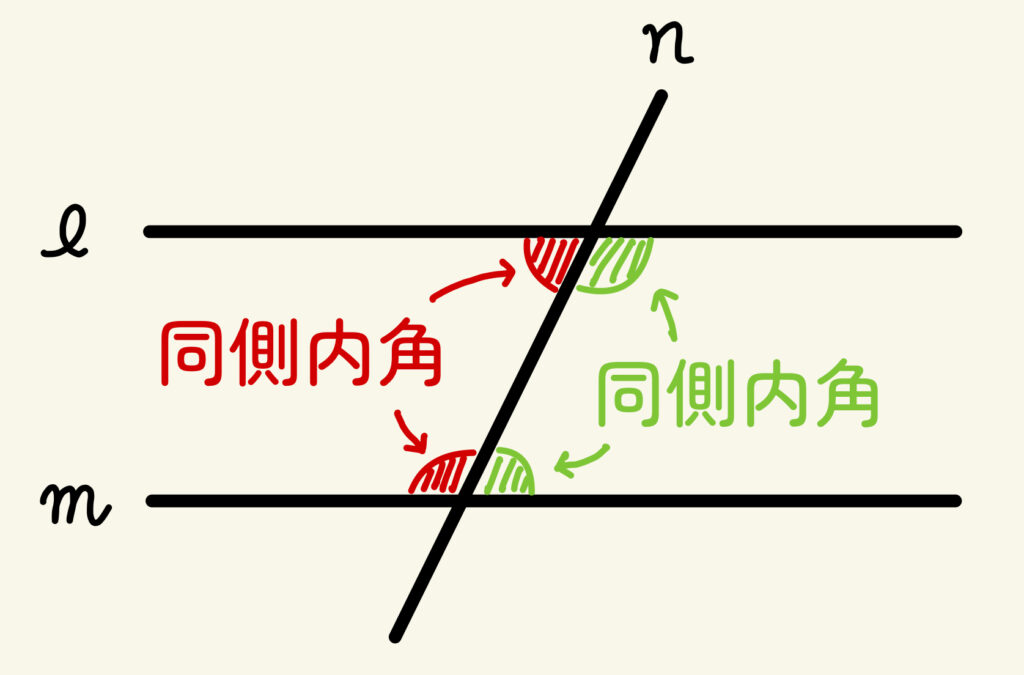
下の図のように、2直線 \(\ell\) 、\(m\) に直線 \(n\) が交わってできる角のうち、赤い印、緑の印のついた位置関係にある角を同側内角といいます。

平行線の同側内角の和は180°

下の図のように、平行な2直線 \(\ell\) 、\(m\) に直線 \(n\) が交わってできる同側内角の和は180°になります。

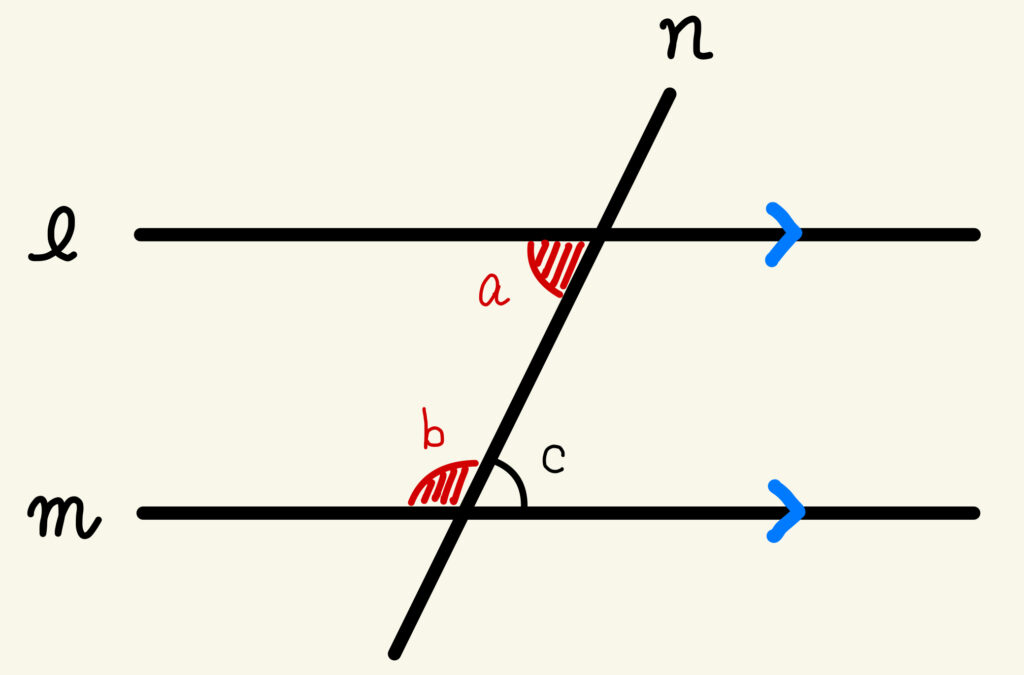
式で表すと、∠\(a\) + ∠\(b\) = 180° となります。

証明

先ほどの図で、
平行線の錯角は等しいから
∠\(a\) = ∠\(c\) …①
直線は180°だから
∠\(b\) ＋ ∠\(c\) ＝ 180° …②
①、②より
∠\(a\) ＋ ∠\(b\) ＝ 180°

平行でなければ和は180°ではない

気をつけてほしいポイントとして、同側内角の和は平行線のときでなければ180°にならないということです。

下の図を見てみましょう。

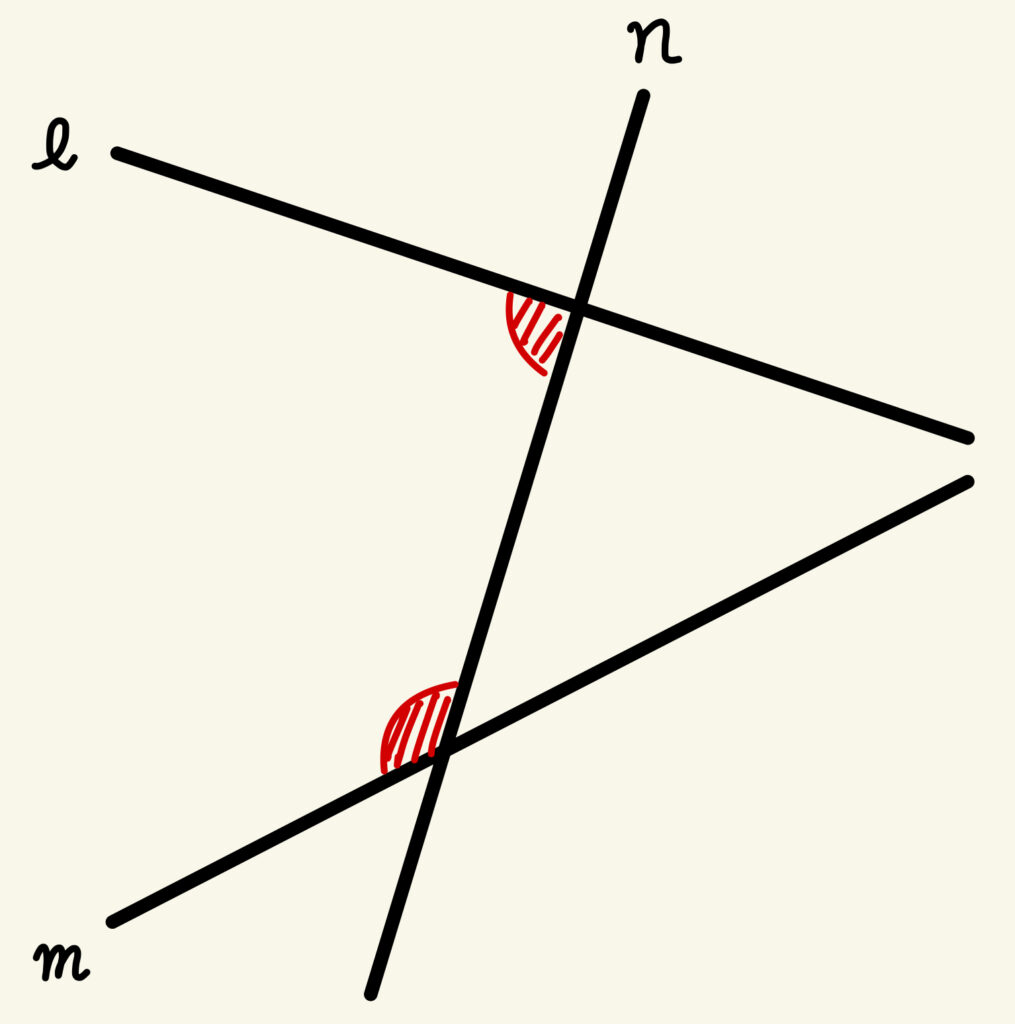
明らかに同側内角の和は180°ではないですね。（180°を超えていますね。）

練習問題

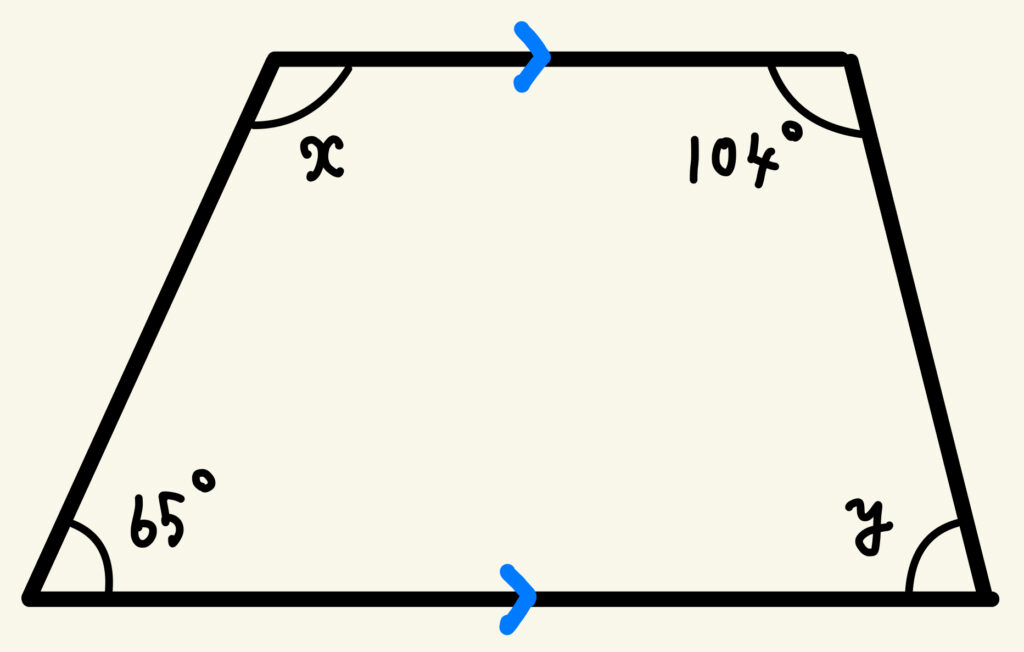
下の図の台形で、∠\(x\) 、∠\(y\) の大きさはそれぞれ何度ですか。

まとめ