円錐の側面積の求め方は？一瞬で求める公式！

円錐の表面積を求めるときに、側面積を求めるのに苦労はしませんでしたか？この記事では、円錐の側面積を一瞬で求める公式を紹介します！

円錐の側面積は「母線×底面の円の半径×\(\pi\)」で一瞬で求められる！

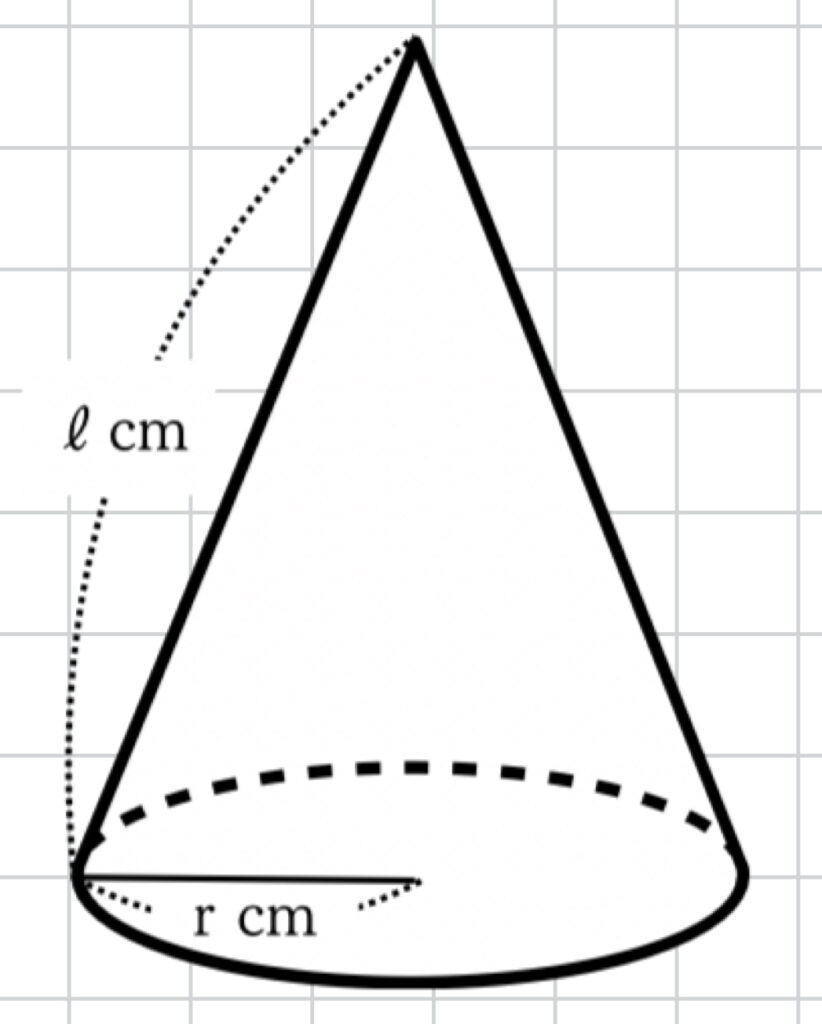
上の図のような、母線が \(\ell\) 、底面の円の半径が \(r\) である円錐の側面積は

で、求めることができます。

なぜこの公式で求められるのか？

母線が \(\ell\) 、底面の円の半径が \(r\) である円錐の展開図は

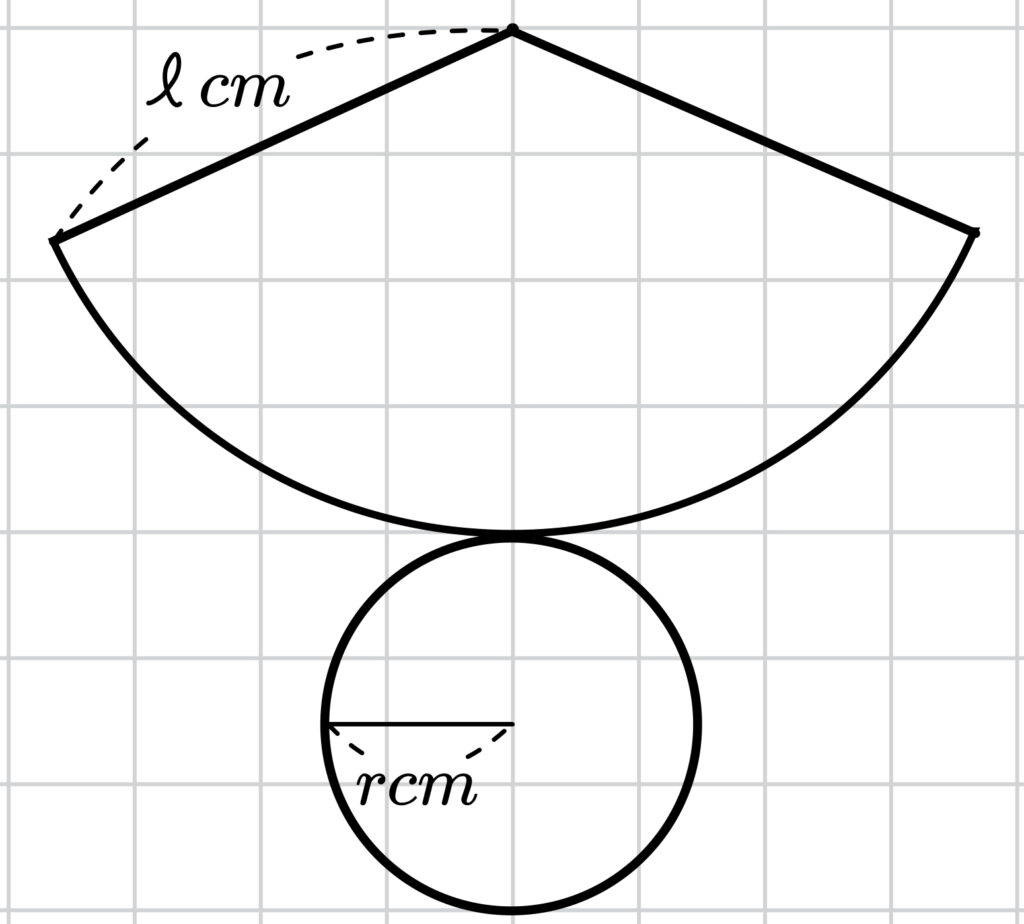
上の図のようになります。

円錐の側面はおうぎ形になるので、おうぎ形の面積を求めます。

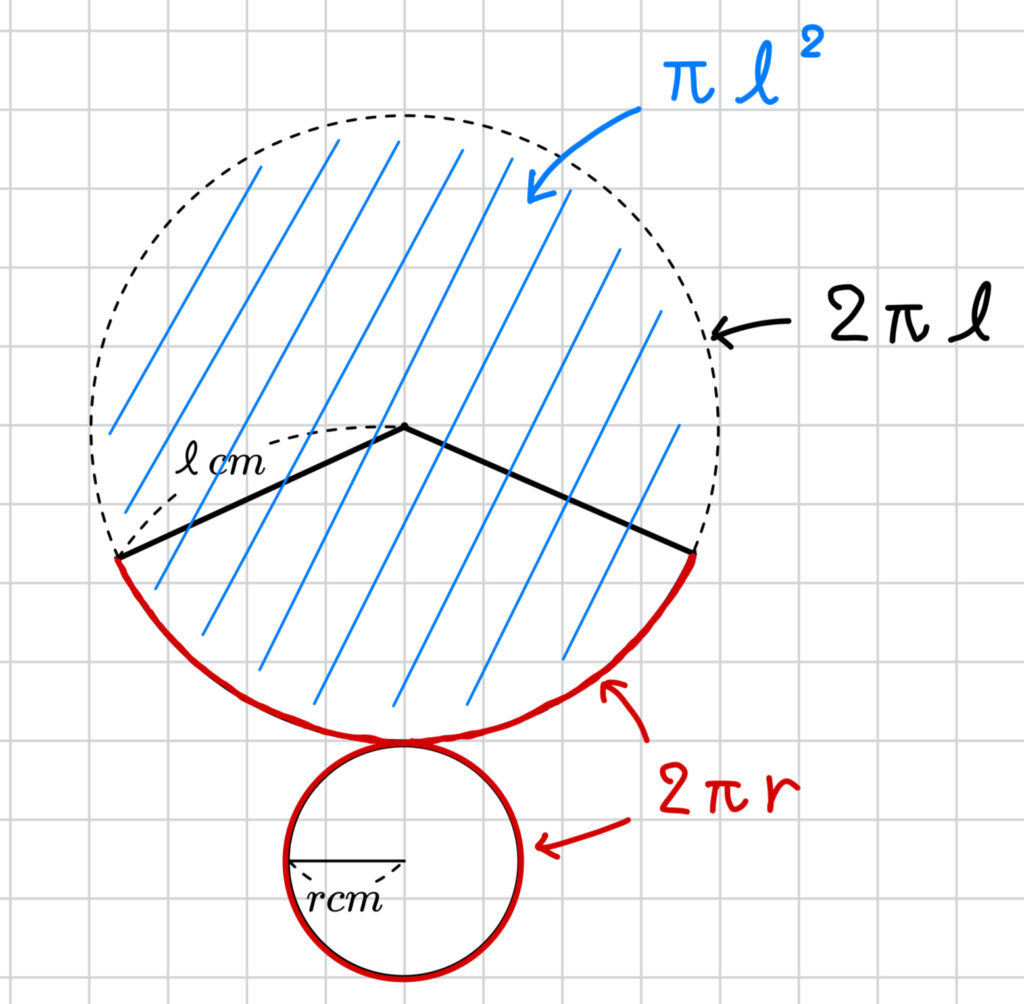
おうぎ形の面積を求めるには、おうぎ形の弧の長さがわかれば求められます。
弧の長さは底面の円の円周と一致するので、（弧の長さ）＝\(\color{red}{2\pi r}\)となります。

そして、弧の長さの、おうぎ形の元の円の円周（\(2\pi \ell\)）に対する割合を求めます。

\(\frac{\color{red}{2\pi r}}{2\pi \ell}=\frac{r}{\ell}\)

となり、求めたいおうぎ形の面積も、おうぎ形の元の円の面積（\(\pi \ell^2\)）の \(\frac{r}{\ell}\) 倍になるので、

（おうぎ形の面積）＝ \( \pi \ell^2\) \(\times \) \(\frac{r}{\ell}\) = \( \ell \times{} r \times{} \pi \)

となるわけです。

実際に公式を使って計算してみよう！

下の図のような、母線が 8cm 、底面の円の半径が 3cm である円錐の側面積を計算します。

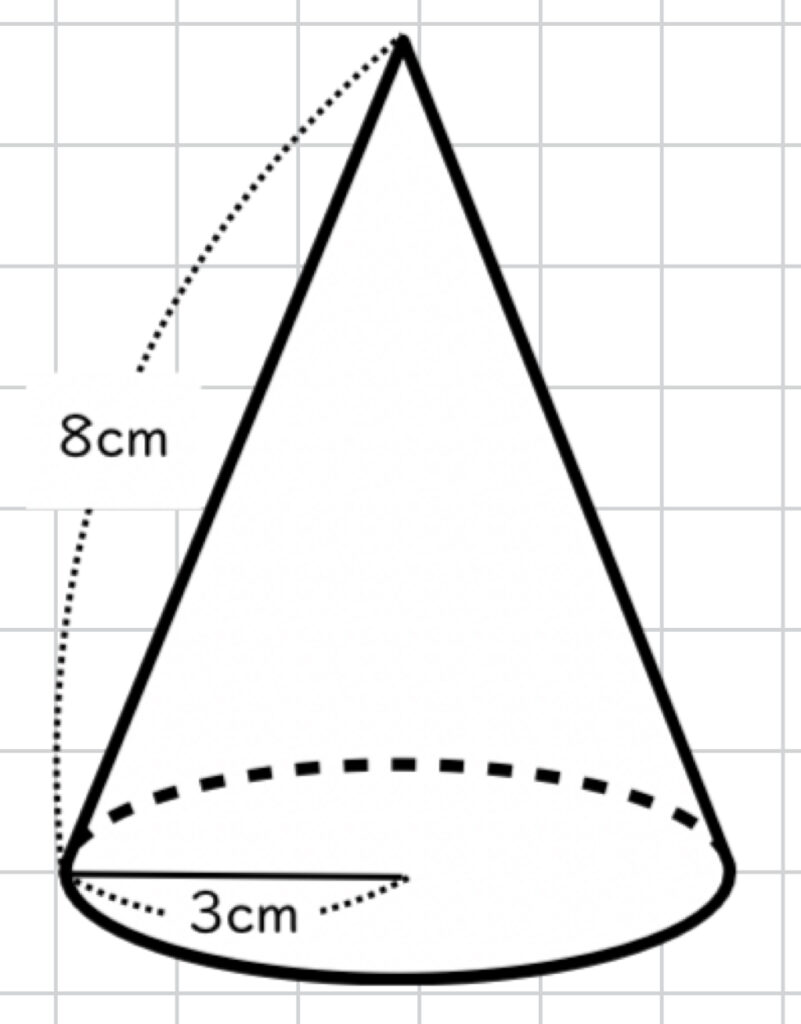
公式にあてはめると、

（円錐の側面積）＝ \( 8 \times {} 3 \times {} \pi \)
＝ \(24\pi\)(㎠)

となります。

数秒で求めることができますね。

教科書通りの求め方と比べてみよう

先ほどの円錐の側面積は、教科書通りの求め方で計算すると次のようになります。

展開図は下の図のようになり、

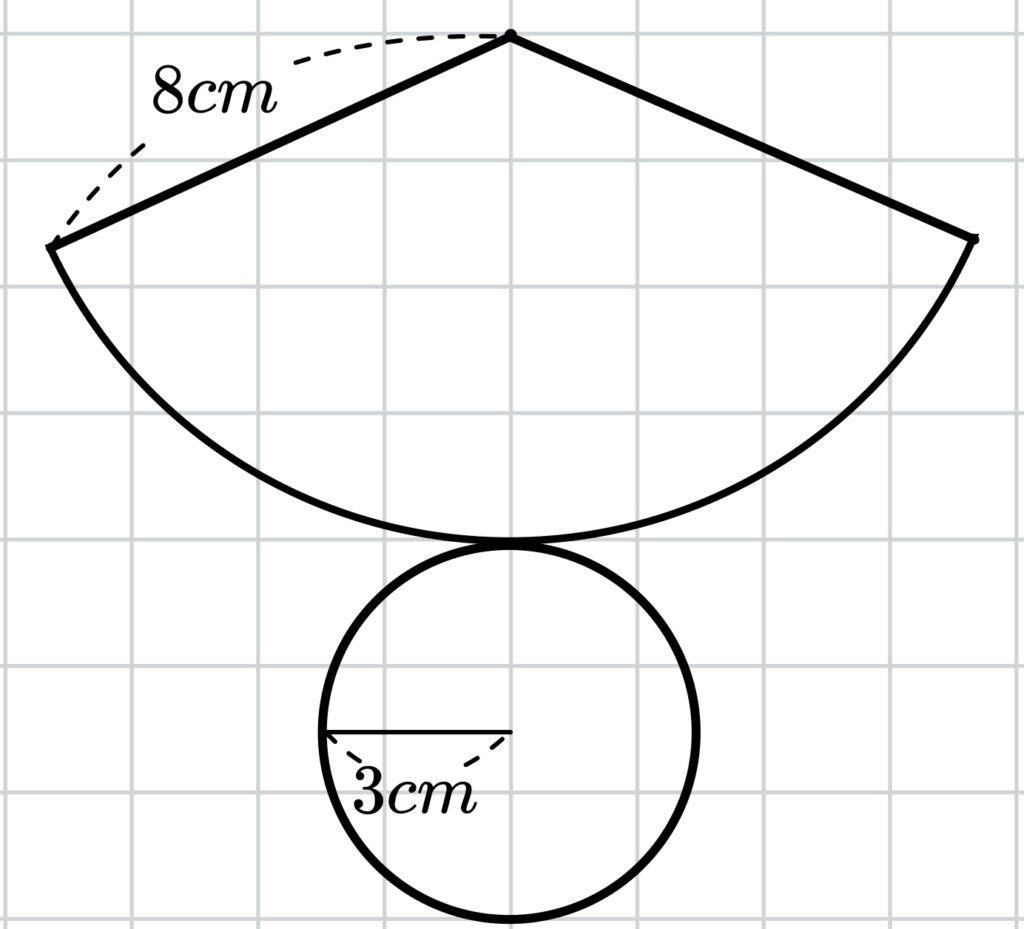
おうぎ形の面積を求めるために、おうぎ形の弧の長さを求めます。
弧の長さは底面の円の円周と一致するので、（弧の長さ）＝\(6\pi\) となります。

そして、弧の長さの、おうぎ形の元の円の円周（\(16\pi\)）に対する割合を求めます。

\(\frac{6 \pi}{16 \pi}\) = \(\frac{3}{8}\)

となり、求めたいおうぎ形の面積も、おうぎ形の元の円の面積（\(64\pi\)）の\(\frac{3}{8}\)倍になるので、

（おうぎ形の面積）＝ \(64\pi \times\)\(\frac{3}{8}\)
＝\(24\pi\)(㎠)

となります。

求め方を思い出しながら計算するとなると、数分かかるかもしれません。

まとめ