中1で学習する素数。その素数を「エラトステネスのふるい」を使って調べたことがあるかもしれません。この方法は、素数を効率よく見つけるために使う方法です。
この記事では、エラトステネスのふるいを使った素数の見つけ方、なぜ6の倍数で改行しているのかを解説していきます!
「エラトステネスのふるい」とは
たとえば、100までの素数を調べるとき、エラトステネスのふるいでは次のようなステップを踏んで素数以外の数をふるい落としていきます。
❶. 「1」は素数ではないので、最初から消しておく。
❷. 残った数の中で最小の素数「2」を◯で囲み、「2」以外の2の倍数を消す。
❸. 残った数の中で最小の素数「3」を◯で囲み、「3」以外の3の倍数を消す。
❹. 残った数の中で最小の素数「5」を◯で囲み、「5」以外の5の倍数を消す。
❺. …(以下同様)
この方法を使うと、残った数がすべて素数になります。
この「ふるい」はよく、6の倍数で改行されたものを使うことが多いですが、なぜ6の倍数で改行すると見やすくなるのでしょうか?その理由を説明します。
6の倍数で改行すると見やすい理由
実は、2と3以外の素数は、すべて次のような形で現れます。
ここで、\(6n-1\) 、\(6n+1\)は1から始まる整数です。これはどういうことか、具体的に説明しますね。
1. 6の倍数の数は素数ではない
6の倍数、つまり6、12、18、24、・・・のような数は、必ず2の倍数か3の倍数です。だから、これらの数は素数ではありません。
2. 6の倍数の前後に素数が現れる
6の倍数の前後には、素数が現れることがよくあります。たとえば
• \(6 \times 1 = 6\) の隣:5(素数)、7(素数)
• \(6 \times 2 = 12\) の隣:11(素数)、13(素数)
• \(6 \times 3 = 18\) の隣:17(素数)、19(素数)
このように、6の倍数を基準にすると、素数が規則的に現れる位置がわかりやすくなるんです。
10の倍数で改行したふるいの例
10の倍数で改行したふるいでは、実際にどのようなふるい落とし方になるでしょう。
下の図を見てください。
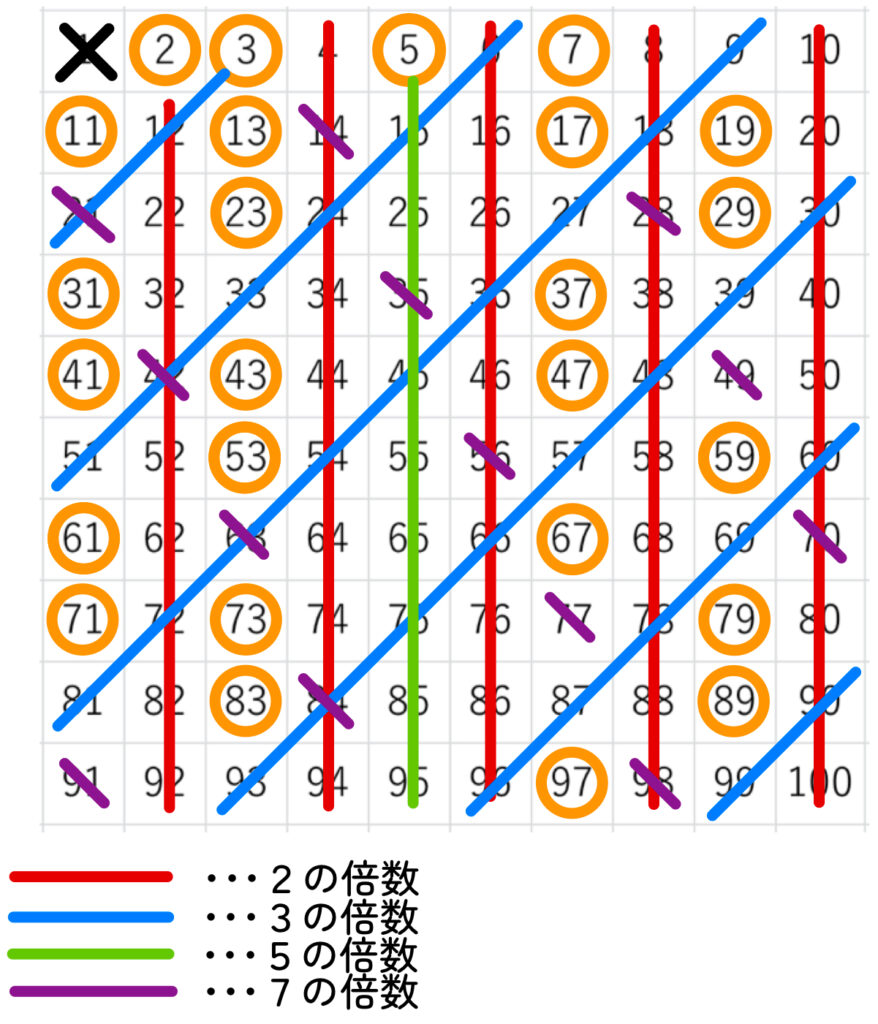
このように並べると、7の倍数を直線で消すことができず、ふるい落としづらいことがわかります。
6の倍数で改行したふるいの例
では、実際に100までの数を6の倍数ごとに改行して並べてみましょう。
下の図のように並べると、倍数がどこにあるかがわかりやすくなります。
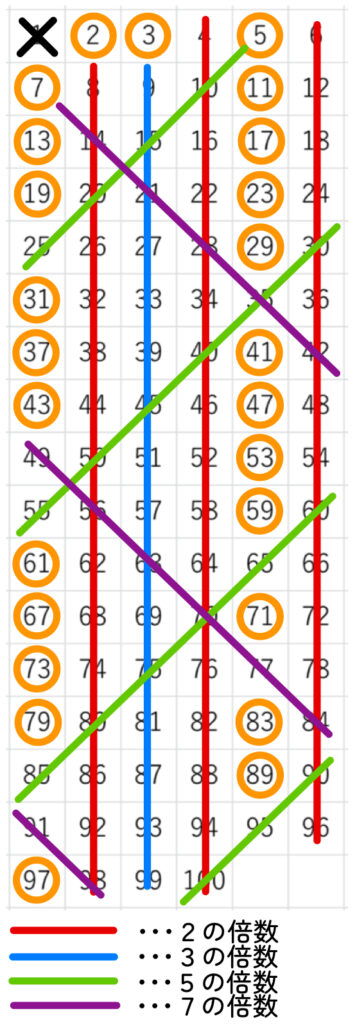
このように並べると、6の倍数(6, 12, 18, …)は素数ではなく、またその前後に素数が現れるのがわかります。
100までの素数を見つける方法
エラトステネスのふるいでは、100までの素数を調べる場合、6の倍数の近くに素数が現れることを活用して効率よくふるい落とすことができました。
また、7の倍数までふるい落とせば、11の倍数はふるい落とす必要はありません。
なぜなら
・11×2=22 は2の倍数でふるい落としている。
・11×3=33 は3の倍数でふるい落としている。
……
・11×11=121 は100を超えている。
つまり、100以下の素数については、7の倍数までの素数の倍数だけをふるい落とせばいいのです。
実際に100までの素数を求めてみると、次のようになります。
100までの素数は:2、3、5、7、11、13、、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97
これが、100までの素数です!
ふるいを使って、このように簡単に素数を見つけることができます。
まとめ
● 「エラトステネスのふるい」を使うと、効率よく素数を見つけることができる。
● 数の並べ方は、6の倍数で改行すると、ふるい落としやすくなる。
ぜひ、エラトステネスのふるいを使って、100より大きい素数も調べてみてくださいね!
にほんブログ村




コメント