小学校では「 \(x\) が2倍、3倍、…と変化すると、それにともなって \(y\) の値も2倍、3倍、…と変化すれば比例」と学習しませんでしたか?
実は、その判断方法は間違っています!では、比例かどうかを正しく判断する方法とは?
比例の定義とは?
まず、数学における 比例の定義 を確認しましょう。
\(y\) が \(x\) の関数で、 \(y=ax\) の形で表されるとき \(y\) は \(x\) に比例するという。
「 \(y\) が \(x\) に比例する」というためには、\(y\) を \(x\) の式で表して、その式が \(y=ax\) の形になっている必要があるのです!
「\(y\) が2倍、3倍、…になっている = 比例」ではないのはなぜ?
「 \(x\) が2倍、3倍、…と変化すると、それにともなって \(y\) の値も2倍、3倍、…と変化すれば比例」というイメージを持ちがち。
確かに、次のような \(x\) と \(y\) の関係は比例に見えます。
| \(x\) | 1 | 2 | 3 | 4 | … |
| \(y\) | 2 | 4 | 6 | 8 | … |
しかしこれは、あくまで「表」で見て、変化の仕方が \(x\) が2倍、3倍、…と変化すると、それにともなって \(y\) の値も2倍、3倍、…と変化しているだけで、「式」をつくって判断していないのです!
\(x\) が2倍、3倍、…と変化すると、それにともなって \(y\) の値も2倍、3倍、…と変化するのは、 比例だったらいえる性質 なんです!比例かどうかを判断する方法ではないのです!
\(y\) が2倍、3倍、…になっているのに比例ではない例
\(x\) が2倍、3倍、…と変化すると、それにともなって \(y\) の値も2倍、3倍、…と変化しているのに、\(y\) が \(x\) に比例していない例は次のようなものです。
| \(x\) | 1 | 2 | 3 | 4 | … |
| \(y\) | 2 | 4 | 6 | 8 | … |

あれ?さっきと同じでは…?
と思われたかもしれませんが、実はこれはガウス記号で表された関数(床関数やフロアー関数という)である、\(y=2[x]\) という式の関数なのです。
\([x]\) は、\(x\)を超えない最大の整数を表す。
たとえば、\([x]\) において
・\(x=1\) のとき、\([x]=1\)
・\(x=1.1\) のとき、\([x]=1\)
・\(x=1.2\) のとき、\([x]=1\)
・\(x=1.9\) のとき、\([x]=1\)
となります。
ですから、\(y=2[x]\) の先ほどの表を詳しく見てみると、
| \(x\) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | … |
| \(y\) | 2 | 2 | 4 | 4 | 6 | 6 | 8 | 8 | … |
であり、 \(x\) が2倍、3倍、…と変化しているのに、 \(y\) の値が2倍、3倍、…と変化していないところがあることがわかります。
\(y=2[x]\) のグラフは次のようになります。
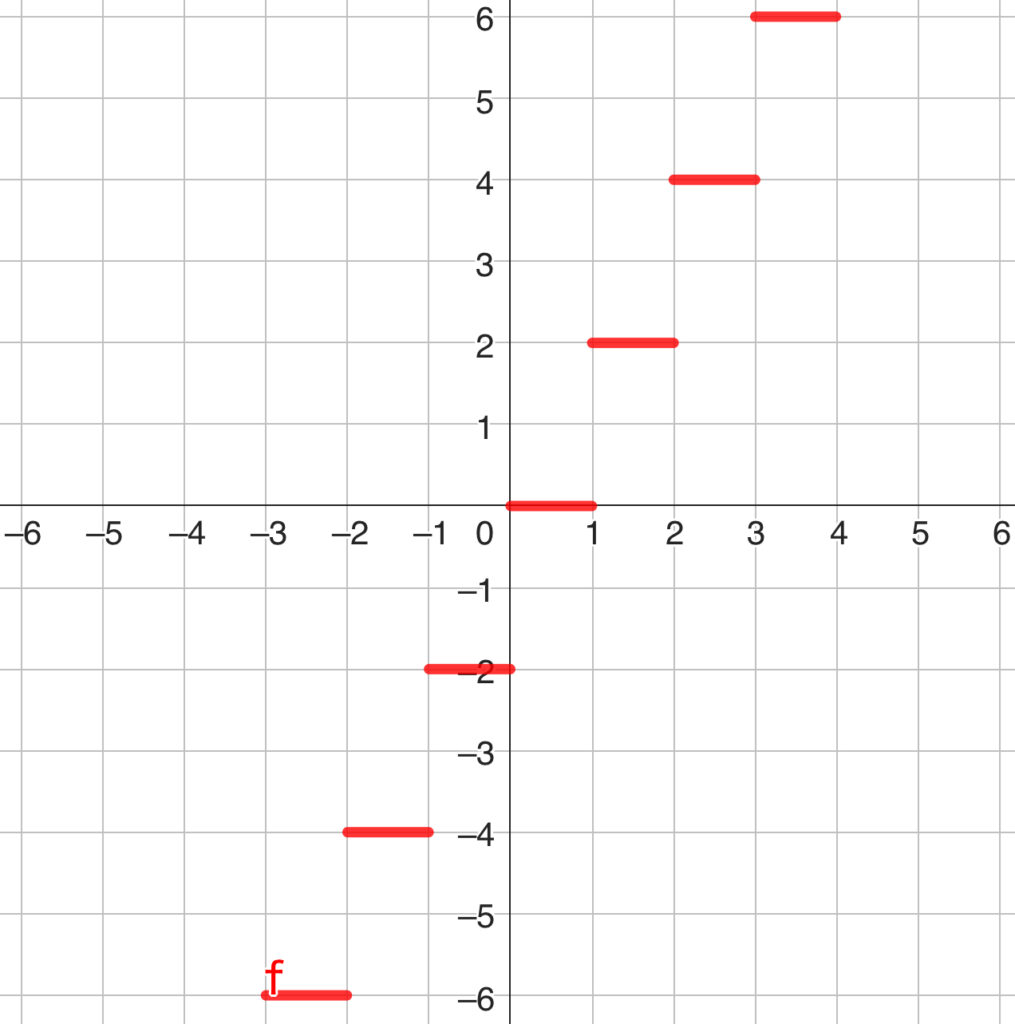
明らかに、比例のグラフではありませんよね。
ですから、「 \(y\) が \(x\) に比例する」というためには、\(y\) を \(x\) の式で表して、その式が \(y=ax\) の形になっているかどうかで判断するのです!
練習問題
1本90円のえんぴつ \(x\) 本と120円の消しゴムを1個買ったときの代金の合計を \(y\) 円とする。
\(x\) と \(y\) の関係について、Aさんは次のように考えた。この考えが間違っている理由を説明しなさい。
\(x\) が大きくなると \(y\) も大きくなるから、 \(y\) は \(x\) に比例している。
hint : \(y\) を \(x\) の式で表すと、 \(y=ax\) の式の形になるかな?
まとめ
● 「 \(x\) が2倍、3倍、…と変化すると、それにともなって \(y\) の値も2倍、3倍、…と変化すれば比例」は間違い!
● ガウス記号を含む関数(床関数)のような、特殊な関数もある!
● \(y\) を \(x\) の式で表して、その式が \(y=ax\) の形になっているかどうかで判断する!
数学では 「なんとなくの感覚」ではなく、定義に基づいて正しく判断することが大切 です!
にほんブログ村




コメント