中1で習う「比例式」。\(x:16 = 12:32\) の \(x\) の値を求めるときに、「内内外外」で計算すると学習したと思います。
しかし、内内の \(16\times12\) を単純に計算してはいませんでしたか?
それでは計算ミスも起こりやすく、計算スピードも遅くなってしまいます。
この記事では、「比例式」を簡単に素早く、ミスのないように計算する方法を解説します!
比例式とは
比例式とは
\(a:b = c:d \)
のような式のことをいいます。
この式は、「 \(a \) と \(b\) の比」と「 \(c\) と \(d \) の比」が等しい ことを表しています。
基本は「内内外外」で計算する!
比例式を解く基本は「内内外外」の関係を使うことです。
始めに出てきた比例式を考えてみます。
\(x:16 = 12:32\)
この比例式では、“=の 内側の積 と 外側の積 が等しくなる”という関係(これが「内内外外」と呼ばれる)を使って方程式になおします。具体的には
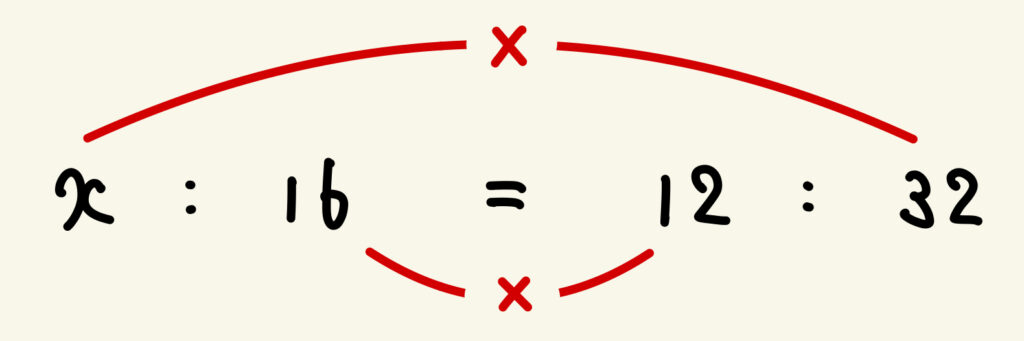
\(32x = 16\times12\)
という方程式の形にします。あとはこれを計算すればOK!
\(32x = 192\)
\(\displaystyle \frac{32x}{32} = \displaystyle \frac{192}{32}\)
\(x = 6\)
これが比例式の基本的な解き方です。
テクニック1:先に比を簡単にして計算を楽にする
先ほどの計算の中で、\(16\times12\) や \(\displaystyle \frac{192}{32}\) はどのように計算しましたか?おそらく筆算をしたのではないでしょうか?ただし、筆算はすればするほど時間がかかるし計算ミスも多くなりますよね。
そこで、比例式では「内内外外」をする前に、比をできるだけ簡単な整数比にしておくと計算が楽になります。
たとえば、先ほどの比例式を考えてみましょう。
\(x:16 = 12:32\)
このまま「内内外外」で計算してもいいですが、右辺の比を簡単にすることで計算がぐっと楽になります。右辺の 12 と 32 を 4 で約分する(正確には”約分”とは言いませんが約分のような操作をするので約分と表現します)と、
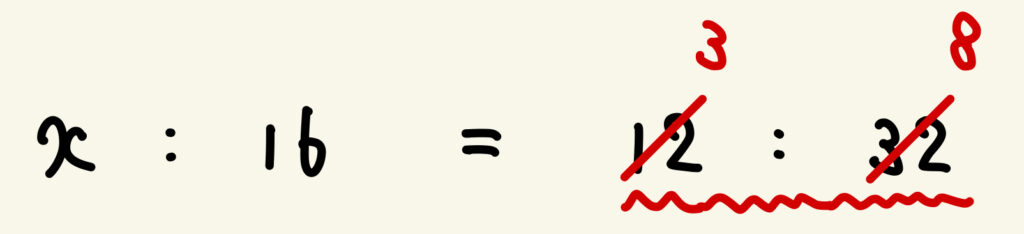
\(x:16 = 3:8\)
となります。ここで「内内外外」を使えば、
\(8x = 16\times3\)
\(8x = 48\)
\(x = 6\)
と、より簡単に \(x\) の値を求めることができました!
このように、先に比を簡単にしてから計算するのがポイントです。
テクニック2:両辺の比の 左どうし、右どうしを先に約分する
先ほどのテクニックは小学校や中学校の授業で習った内容かもしれません。
ここでは、さらなるテクニックを紹介します。
それは、比例式では「内内外外」で計算をする前に、両辺の比の「左どうし」「右どうし」を先に約分します。これを使うと、さらに計算が楽になります。
たとえば、先ほどの比例式を考えてみましょう。
\(x:16 = 12:32\)
この比例式では、両辺の右どうし、つまり 16 と 32 が 16 で約分できるので約分をします。すると、

\(x:1 = 12:2\)
となります。ここで「内内外外」を使えば、
\(2x = 12\)
\(x = 6\)
となり、テクニック1より簡単に \(x\) の値を求めることができました!
このように、先に両辺の比の「左どうし」「右どうし」を約分してから計算するのがポイントです。
なぜ両辺の比の「左どうし」「右どうし」を約分してもいいの?
両辺の比の「左どうし」「右どうし」を先に約分できる理由は、比例式の性質にあります。
\(a:b = c:d \) という比例式では、\(a\) の値を求めるために「内内外外」をして、
\(a \times d = b \times c\)
両辺を \(d\) で割って
\(a = \displaystyle \frac{b \times c}{d}\)
という関係が成り立つからです。
この関係式から、\(d\) は \(c\) と結局約分をするのだから、先に約分してもいいことがわかります。
→これはテクニック1の右辺の比を簡単にしてもいいということを示していますね。
また、\(d\) は \(b\) とも結局約分をするのだから、先に約分してもいいことがわかります。
→これはテクニック2の両辺の「右どうし」を約分してもいいということを示しています。
同じように考えると、テクニック1の左辺の比を簡単にしてもいいこと、テクニック2の両辺の「左どうし」を約分してもいいことがわかりますね。
ですから、「内内外外」をする前に、両辺の比の「左どうし」「右どうし」を約分してもいいのです。
テクニック1 と テクニック2 を組み合わせる
テクニック1 と テクニック2 を組み合わせると、一切の筆算もせず、簡単な九九の計算だけで比例式を解くことができます。
たとえば、先ほどの比例式を考えてみましょう。
\(x:16 = 12:32\)
テクニック1を使い、12 と 32 を約分します。すると、
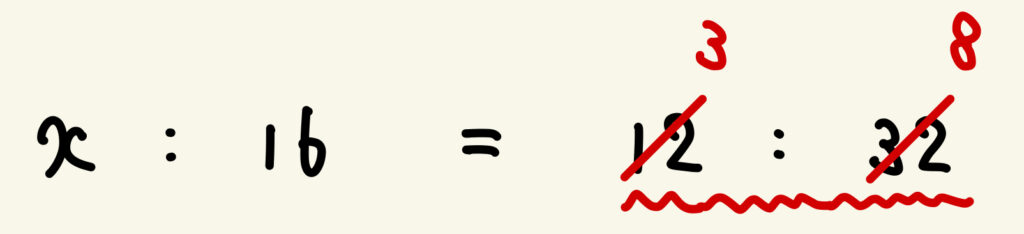
\(x : 16 = 3 : 8\)
そして、テクニック2を使い、両辺の比の「右どうし」を約分します。すると、
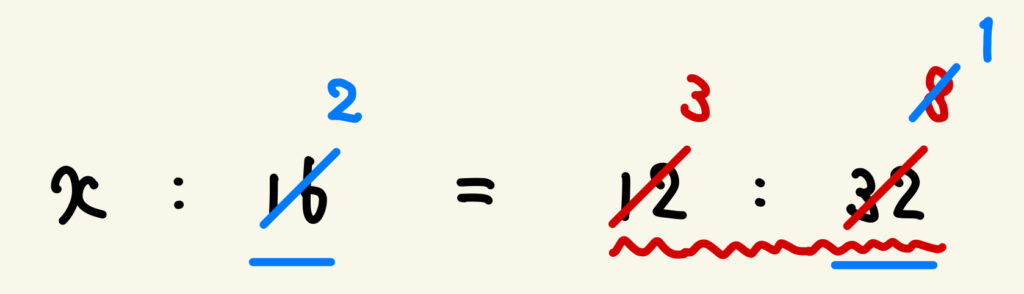
\(x : 2 = 3 : 1\)
最後に「内内外外」をして、
\(x = 6\)
と、最後は \(2\times 3\) をするだけで \(x\) の値を求めることができました!
まとめ
比例式を解くときのポイントを振り返ると
1. 基本は「内内外外」の計算を使う
比例式の “=の内側と外側の積が等しくなる” という関係を使って、方程式にすることで、比例式を解くことができます。
2.比を簡単にしてから計算する
左辺や右辺の比を先に簡単なすることで、計算がぐっと楽になります。
3.両辺の比の左どうし、右どうしを約分する
両辺の比の「左どうし」「右どうし」を先に約分することで、計算をさらに簡単にすることができます。
これらのテクニックを活用して、比例式の問題を効率よく解いてみましょう!
にほんブログ村




コメント