【連立方程式】池の周りで追いつく2人の速さは？

テストや教科書の応用問題でよく出る問題の解説です。

池の周りを走る2人の速さを求める問題

具体的には次のような問題です。

解説

Aくんの速さを分速 \(x\) m、Bさんの速さを分速 \(y\) mとします。

「同じところを同時に出発して、反対の方向にまわると15分後にはじめて出会います。」という情報を図にすると

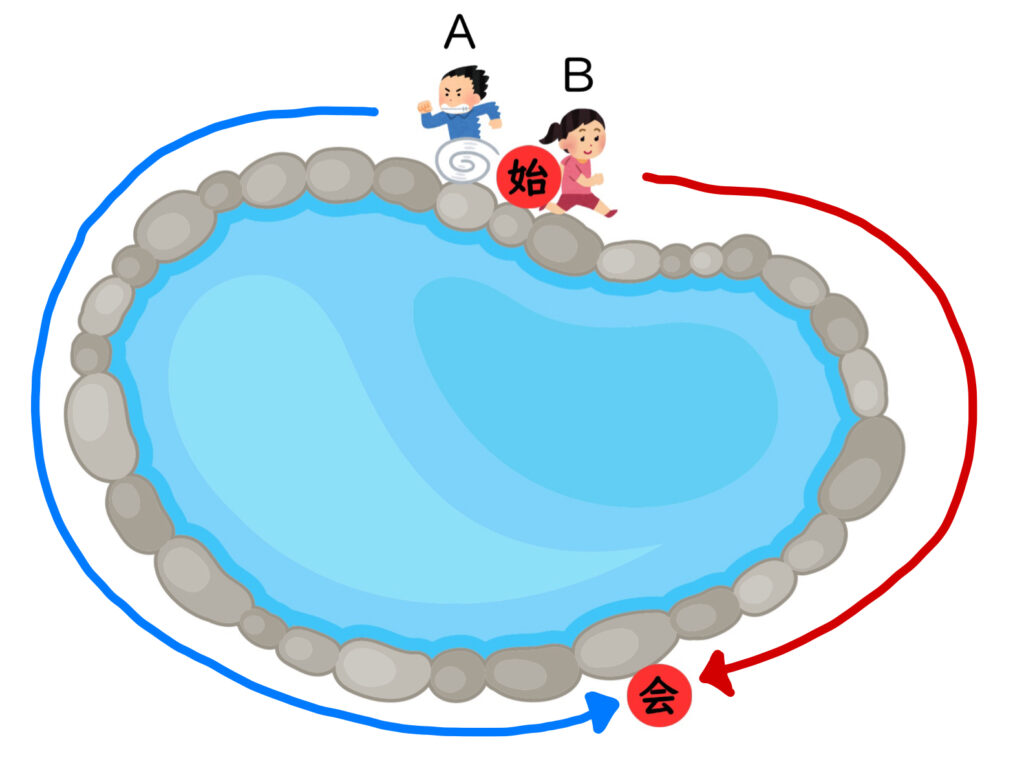
という状態ですから、15分後の2人の進んだ距離の合計が池１周分になる、ということがわかります。
言葉の式にすると
（Aくんの進んだ距離）＋（Bさんの進んだ距離）＝（池１周分）
となります。
数学的な式にすると
\(15x+15y=2700\)
となります。

次に、「同じ方向にまわると、AくんはBさんに45分後にはじめて追いつきます。」という情報を図にすると

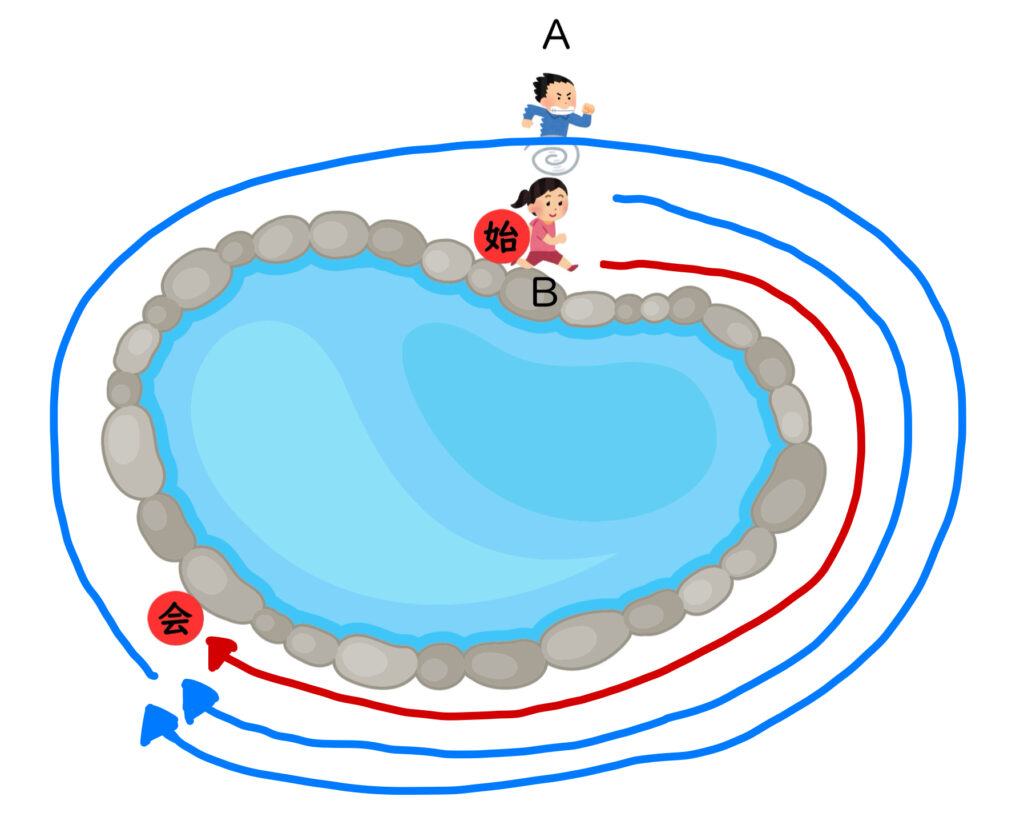
という状態ですから、45分後の2人の進んだ距離の差が池１周分になる、ということがわかります。
言葉の式にすると
（Aくんの進んだ距離）－（Bさんの進んだ距離）＝（池１周分）
となります。
数学的な式にすると
\(45x-45y=2700\)
となります。

この2つの情報から
\(\begin{cases} 15x+15y=2700 \cdots ① \\ 45x-45y=2700 \cdots ②\end{cases}\)
という連立方程式ができますね。
あとは、この連立方程式を解きましょう。

①×3 ＋ ② をして
\(45x+45y=8100\)
\(45x-45y=2700\)
\(\underline{\hspace{5cm}}\)
\(90x = 10800\)
\(x = 120\)

\(x = 120\) を ① に代入
\(15 \times 120 +15y =2700\)
\(1800 +15y =2700\)
\(15y = 900\)
\(y = 60\)

よって、Aくんの速さは 分速120m、Bさんの速さは 分速60m となります。

まとめ