角の三等分線を作図することはできるの？

中学校1年生で学習する作図。そのうちの1つで角の二等分線の作図を学習したと思います。角の二等分線の作図方法やその性質は覚えていますか？
また、角の二等分線が作図できるなら、角の三等分線はどのように作図するのかと疑問に思わないでしょうか？
この記事では、角の二等分線の作図方法や性質を復習し、角の三等分線はどのようにして作図できるのかを紹介していきます！

角の二等分線の作図方法

まず、角の二等分線を作図する手順は次のとおりです。

①. 角の頂点 O を中心として円をかき、角の2辺との交点を C、D とする。

②. C、D をそれぞれ中心として、等しい半径の円をかき、その交点を E とする。

③. 半直線 OE を引く。

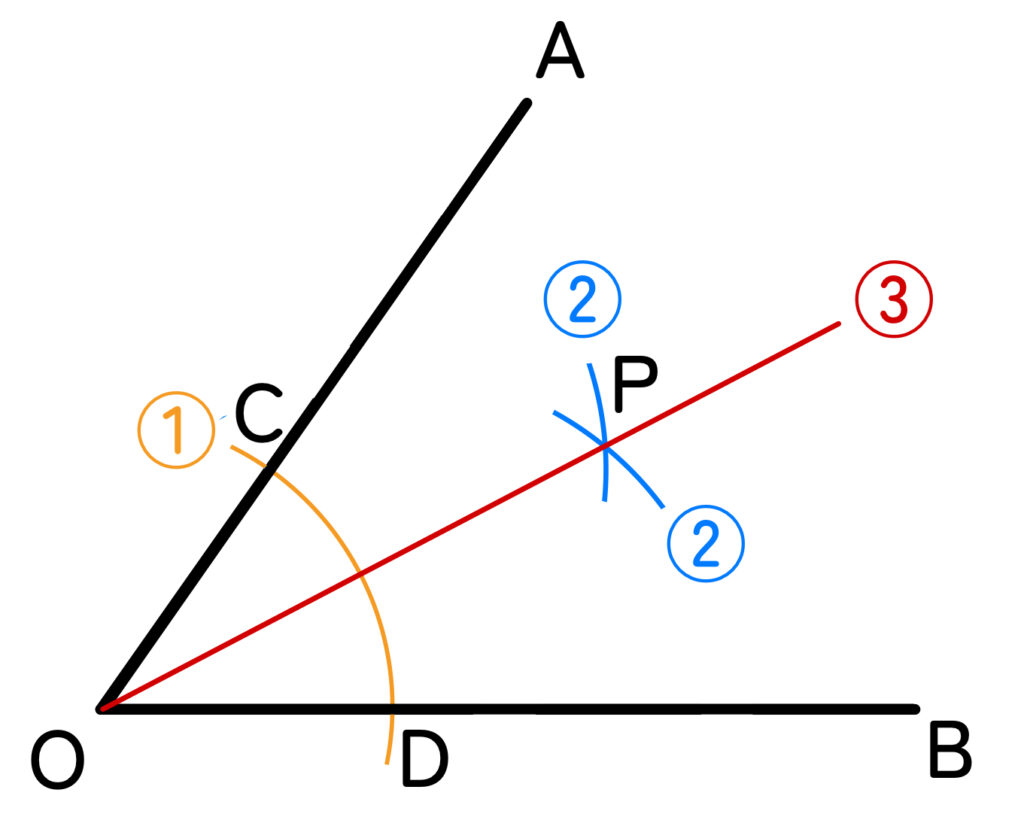
こうしてできた半直線 OE が、角の二等分線です。つまり、角をちょうど半分に分ける線ですね。

角の二等分線の性質

角の二等分線には、次のような性質があります。

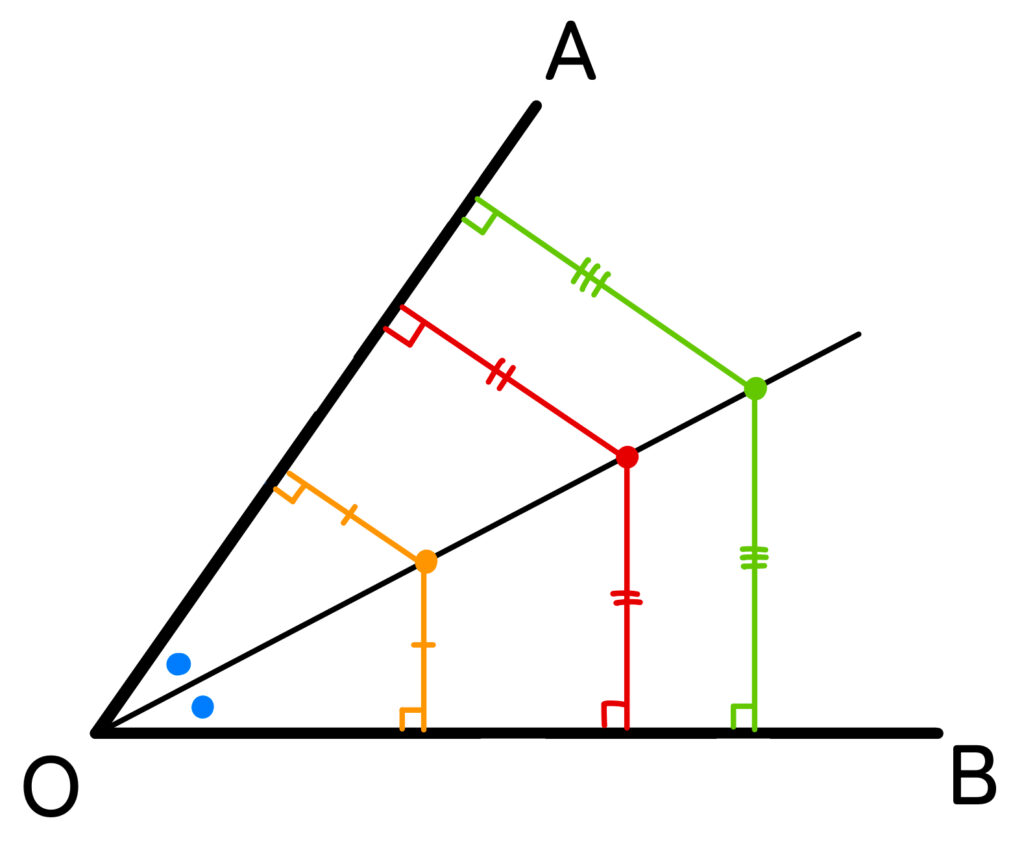
つまり、角の二等分線は角を2つに分けるだけでなく、「２つの辺からの距離が等しい点を見つけられる」という特徴もあるのです。

では、角の三等分線はどう作図する？

「角を三等分する線（角の三等分線）」はどのように作図するのでしょうか？
これも角の二等分線と同じようにコンパスと定規で作図できるのでしょうか？
実は、この問題には驚きの事実が隠されています。
角の三等分線の作図は、なんと……

不可能なのです。

この問題は、約2000年以上前の古代ギリシャ時代から数学者たちが解決に挑戦してきた問題でした。
しかし、19世紀になってフランスの数学者ピエール・ヴァンツェルが、
「コンパスと定規だけでは角の三等分線を作図することはできない」
と数学的に証明しました。

つまり、いくら工夫しても、コンパスと定規だけではこの問題を解くことができないのです。これは、数学の世界では「作図不可能な問題」の代表例として知られています。

折り紙を使うと作図可能！

「コンパスと定規では不可能」でも、実は別の道具を使えば角の三等分線を作図することができます。

その道具とは、なんと…折り紙です！

折り紙を使うと、ある工夫をすることで角の三等分線を作図できることが知られています。
折り紙には「折り」という新しい操作が加わるため、コンパスや定規では不可能だったことが可能になるのです。

興味がある人は、折り紙を使った角の三等分線の作図にぜひ挑戦してみてください！

まとめ