【比例と反比例】電子レンジの加熱時間は出力に反比例！間違いやすい考え方に注意！

コンビニのお弁当にこんな表示が書いてあったこと、ありませんか？

「じゃあ600Wだったら何分何秒加熱すればいいんだろう？」

こうした疑問は、中学数学の「反比例」の関係を使えばバッチリ解決できます！

この記事では、

という流れで、わかりやすく解説していきます！

電子レンジの加熱時間と出力（ワット数）の関係は？

では、さっそく先ほどのお弁当の表示についての問題です。

ありがちな間違い：100W上がるごとに6秒短くなっていく？

こんなふうに考えた人はいませんか？

「1500Wは500Wより1000W高い」

「そのぶん60秒短くなっている」

「じゃあ、100W上がるごとに6秒短くなるってこと？」

「600Wは500Wより100W高いから、90−6＝84秒、つまり1分24秒！」

これは間違いです！

なぜかというと、超高出力の2000Wの電子レンジがあれば、加熱時間が 0秒 でよいことになってしまいます！

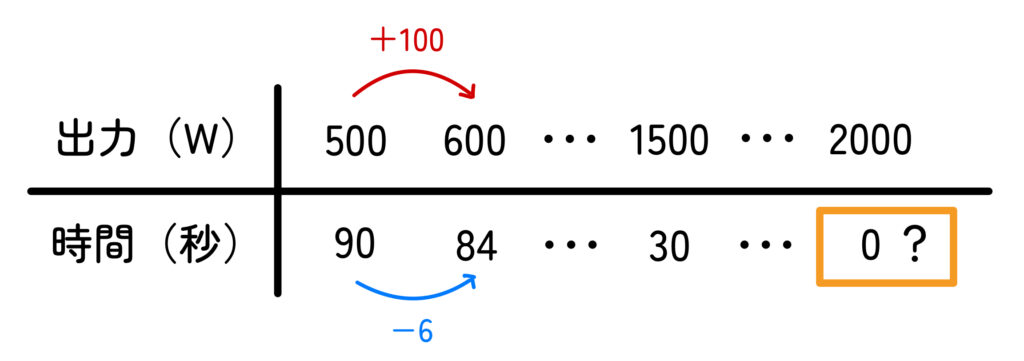
これは明らかにおかしいですよね。

加熱時間と出力は反比例している！

このように、出力が3倍（500→1500）になれば、時間は \(\displaystyle \frac{1}{3}\) 倍（90→30秒）になっています。

ここから、加熱時間は出力に反比例している ということがわかります。

これを使えば、正しく600Wでの加熱時間を求められます。

表や式を使った正しい求め方

表を使った求め方

まずは、出力と時間の関係を表にしてみます。

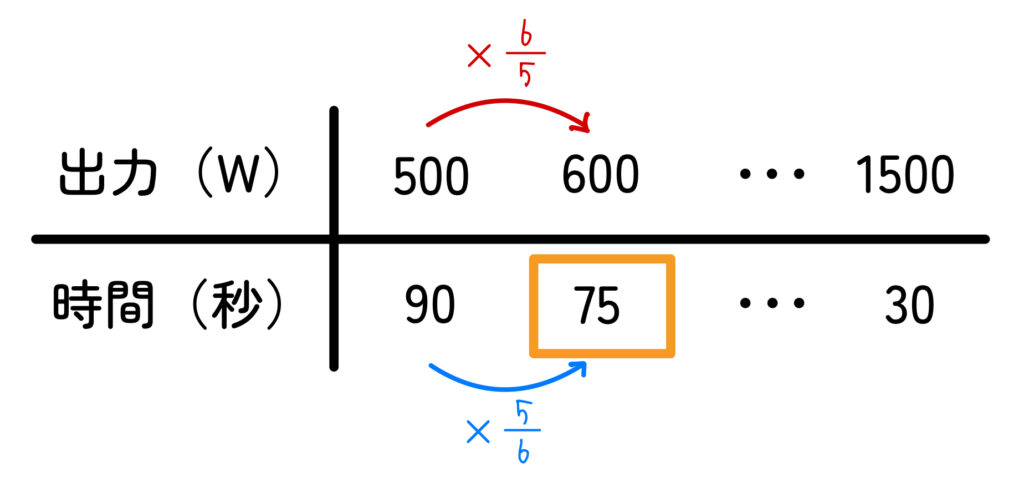
出力の 500Wから600Wは \(\displaystyle \frac{600}{500}\) = \(\displaystyle \frac{6}{5}\) 倍ですから、

加熱時間は出力に反比例するので、逆数である \(\displaystyle \frac{5}{6}\) 倍になります。

よって、

\(90 \times \displaystyle \frac{5}{6} = 75\) 秒

つまり、1分15秒 が適切な加熱時間となります！

式を使った求め方

出力を \(x\) W、加熱時間を \(y\) 秒とすると、加熱時間 \(y\) は出力 \(x\) に反比例するので，

\(y\) を \(x\) の式で表すと、

\(y=\displaystyle \frac{a}{x}\) の形となり、

ここで、比例定数 \(a\) は \(x \times y\) で求められるので、

\(x=500\) W のときの \(y=90\) 秒 を代入して

\(a = 500 \times 90 = 45000\) とわかるので

\(y=\displaystyle \frac{45000}{x}\)

となります。

この式に、\(x=600\) W を代入して

\(y = \displaystyle \frac{45000}{600} = 75\) 秒

つまり、1分15秒 が適切な加熱時間となります！

おまけ：1500Wってなに？

家庭用電子レンジは、だいたい500W〜1000Wあたりが主流です。

でも、「1500W」と表示されていることもありますよね。そんな電子レンジなんてあるの？と思いますよね。

実はこれは、

業務用レンジ（コンビニや飲食店などで使われる）に対応した目安 です。

家庭用のレンジでは、1500Wは出せない機種がほとんど。
でも、説明に「1500Wで30秒」とあると、時間の目安がわかりやすいので書かれていることが多いのです。

まとめ