「割合の文章題ってややこしい…」「連立方程式は立てられるけど、答えが合わない…」そんな経験はありませんか?
この記事では、割合を含む連立方程式の文章題を、表で整理しながら解く方法を紹介します。
さらに、よくある間違いのパターンや、式をどう立てればいいかの考え方まで、しっかり解説します!
表をつくって情報を整理しよう
\(\,\)ある中学校では、毎年ボランティア活動に参加していて、昨年の参加者数は男女合わせて200人でした。今年は、昨年に比べると男子は20%増え、女子は15%減り、全体の参加者数は198人でした。
\(\,\)昨年の男子と女子の参加者数をそれぞれ求めなさい。
割合の文章題のポイントは、表をつくって情報を整理することです。
昨年の男子の人数を \(x\) 人、女子の人数を \(y\) 人とすると
| 男子 | 女子 | 合計 | |
| 昨年の 人数 | \(x\) | \(y\) | 200 |
| ??? | \(\displaystyle \frac{20}{100}x\) | \(−\displaystyle \frac{15}{100}y\) | 198 |
となり、次のような連立方程式ができます。
\(\begin{cases} x+y=200 \\ \displaystyle \frac{20}{100}x − \displaystyle \frac{15}{100}y =198 \end{cases}\)
しかし、この連立方程式は間違いです。
なぜなら、下の方程式の左辺は「増えた人数」を表しているのに、右辺は「今年の人数」になっているからです。
増えた人数は、2人減った(200→198)ので「-2」となるので、正しく表をつくると
| 男子 | 女子 | 合計 | |
| 昨年の 人数 | \(x\) | \(y\) | 200 |
| 増えた 人数 | \(\displaystyle \frac{20}{100}x\) | \(−\displaystyle \frac{15}{100}y\) | -2 |
となり、正しい連立方程式は
\(\begin{cases} x+y=200 \\ \displaystyle \frac{20}{100}x − \displaystyle \frac{15}{100}y =−2 \end{cases}\)
となります。
割合の文章題では、2元1次方程式が3つ立てられる!
実は、もう1つ、今年の人数をそのまま方程式にする方法もあります。
・男子は昨年の \(x\) 人より20%増えたので、今年は \(\displaystyle \frac{120}{100}x\) 人
・女子は昨年の \(y\) 人より15%減ったので、今年は \(\displaystyle \frac{85}{100}y\) 人
ですので、
| 男子 | 女子 | 合計 | |
| 昨年の 人数 | \(x\) | \(y\) | 200 |
| 増えた 人数 | \(\displaystyle \frac{20}{100}x\) | \(−\displaystyle \frac{15}{100}y\) | -2 |
| 今年の 人数 | \(\displaystyle \frac{120}{100}x\) | \(\displaystyle \frac{85}{100}y\) | 198 |
という表になり、次のように3つの正しい方程式が立てられます。
\(\begin{cases} x+y=200 \\ \displaystyle \frac{20}{100}x − \displaystyle \frac{15}{100}y =−2 \\ \displaystyle \frac{120}{100}x + \displaystyle \frac{85}{100}y =198 \end{cases}\)
このうちどれか2つの方程式を連立すれば、正しい答えにたどり着きます。
大事なのは
どの式も、何についての方程式を立てているのか意識すること!
意味の異なる数量についての方程式を立てると、間違った連立方程式になります。
連立方程式を解いてみよう
「昨年の人数」と「増えた人数」についてつくった連立方程式

「昨年の人数」と「今年の人数」についてつくった連立方程式
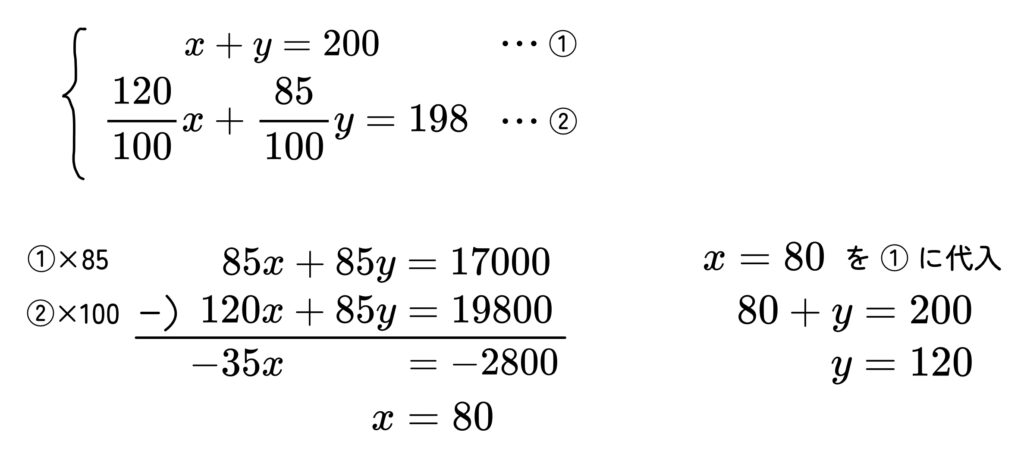
どちらも、答えは
昨年の男子→80人、昨年の女子→120人
となっていますね。
まとめ
割合の文章題では
● 表をつくって情報を整理すること!
● 表につくるときは、何の数量についてまとめているのか、式の意味をよく考えること!
● 2元1次方程式は3つ立てたれるので、そのうち2つを立てて連立すればいい!
にほんブログ村




コメント