【連立方程式】解の比からaの値を求める問題はどのように解けばいい？【解説】

テストや教科書の応用問題でよく出る問題の解説です。

連立方程式の解の比が与えられていて \(a\) の値を求める問題

具体的には次のような問題です。

解説

1．解の比の情報から方程式をつくる

まず、解の比が \(x:y=2:3\) であるとわかっているので、比例式の性質を使って方程式をつくります。

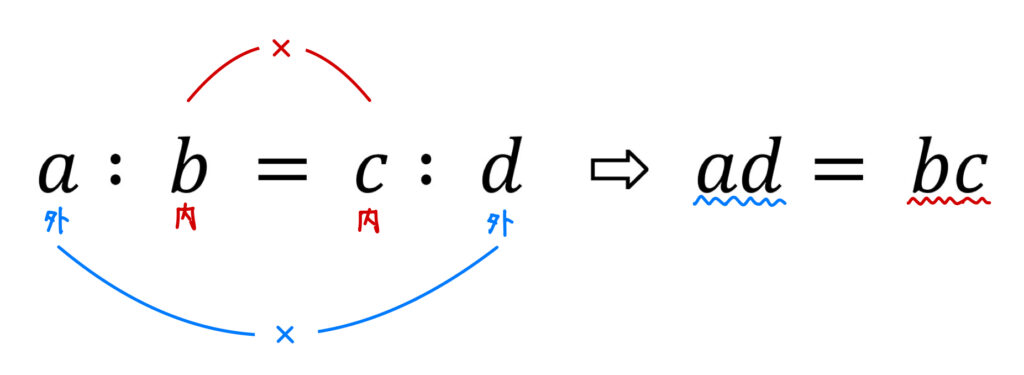
“内内外外”をして、
\(3x=2y\) となります。
この後、加減法を使いたいので、\(2y\) を左辺に移項して
\(3x-2y=0\) …③

２．\(a\) をふくまない方程式と連立方程式にして解く

ここで、\(a\) をふくまない方程式である①の方程式と、先ほどの③の方程式を組み合わせて
\(\begin{cases} 7x-4y=4\,･･･① \\ 3x-2y=0\,･･･③ \end{cases}\)
と連立方程式をつくり、これを解くと

①－③×2 をして
\(7x-4y=4\)
\(6x-4y=0\)
\(\underline{\hspace{5cm}}\)
\(x = 4\)

\(x = 4\) を ③ に代入
\(3 \times 4 -2y =0\)
\(12 -2y =0\)
\(-2y = -12\)
\(y = 6\)

３．求めた \(x\)、 \(y\) の値を \(a\) をふくむ式に代入

\(x=4,y=6\) とわかったので、\(a\) をふくむ方程式である②の方程式に代入します。

\(ax-3y=2\) …②
\(a \times 4-3\times6 =2\)
\(4a-18=2\)
\(4a=20\)
\(a=5\)
となります。

まとめ

解の比から \(a\) の値を求める問題は

という手順で、解決することができます！