【三平方の定理】立方体の対角線の長さは？【証明】

下の図のような1辺が \(a\,cm\)の立方体の対角線の長さは \(\sqrt{3} \,a\) になることが知られています。

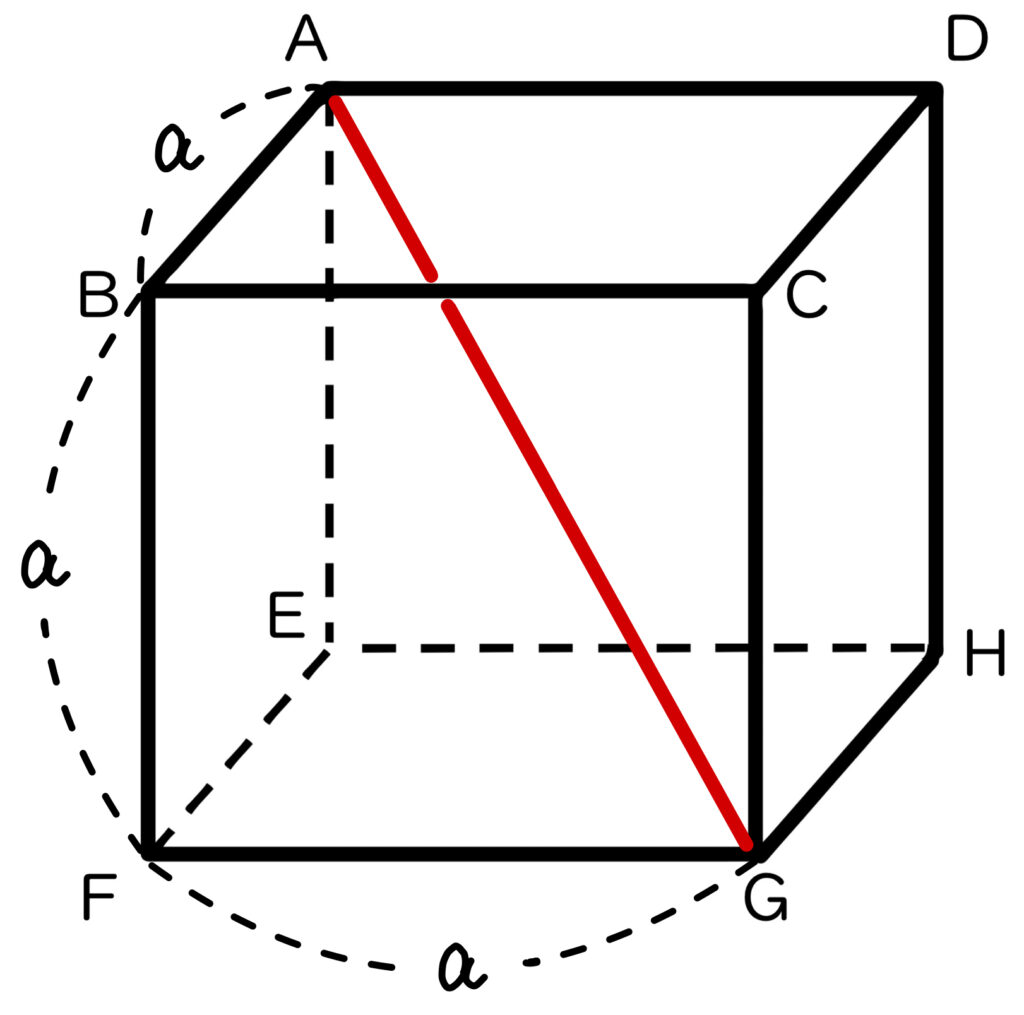
この記事では、なぜ立方体の対角線の長さが \(\sqrt{3} \,a\) になるのか、三平方の定理を使った証明を紹介します！

証明

対角線 \(AG\) を求めるためには、\(AG\) を含む直角三角形があればよい（三平方の定理が使える！）ので、△\(AEG\) をつくります。

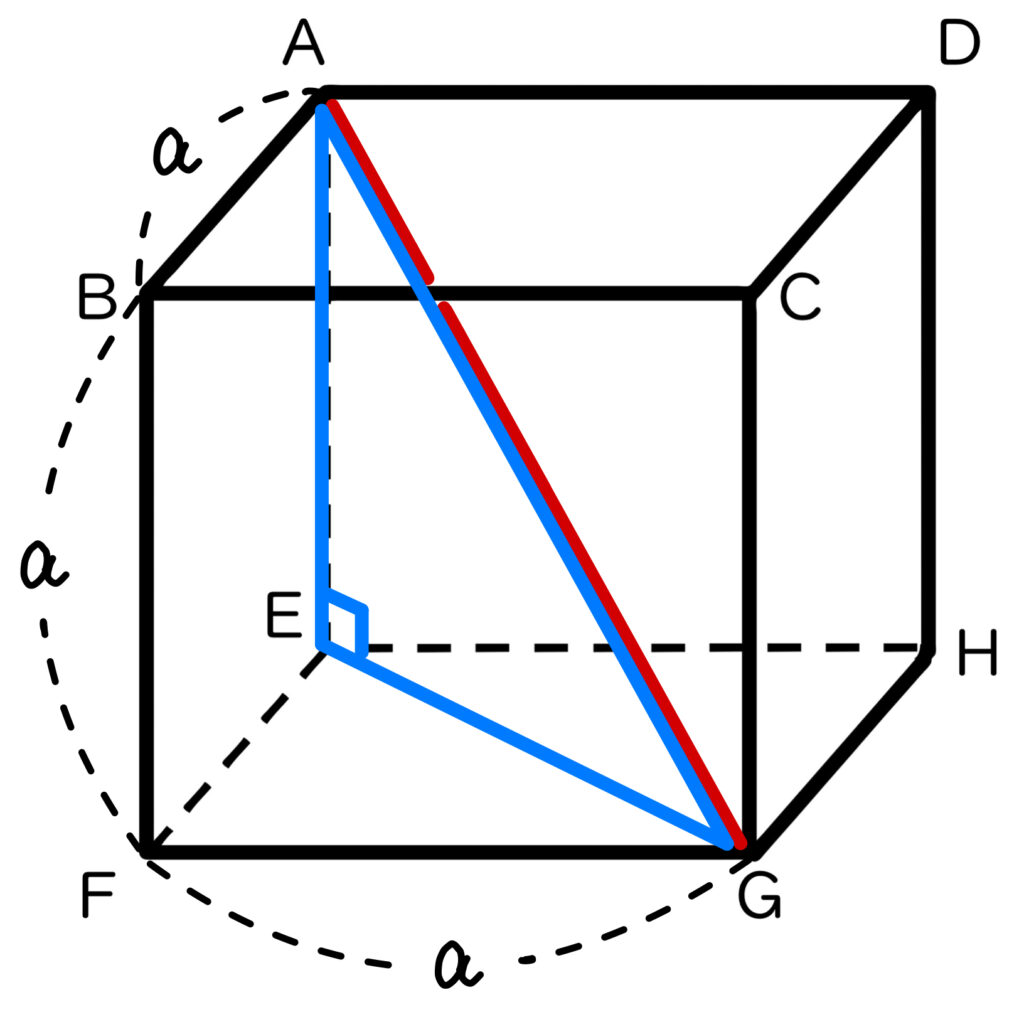
△\(AEG\) は直角三角形なので、三平方の定理より
\(AE^2 \,+ \,EG^2\,=\,AG^2\) … ① が成り立ちます。

しかし、\(EG\) の長さがわかりません。

そこで、\(EG\) を求めるためには、\(EG\) を含む直角三角形があればよいので、△\(EFG\) をつくります。

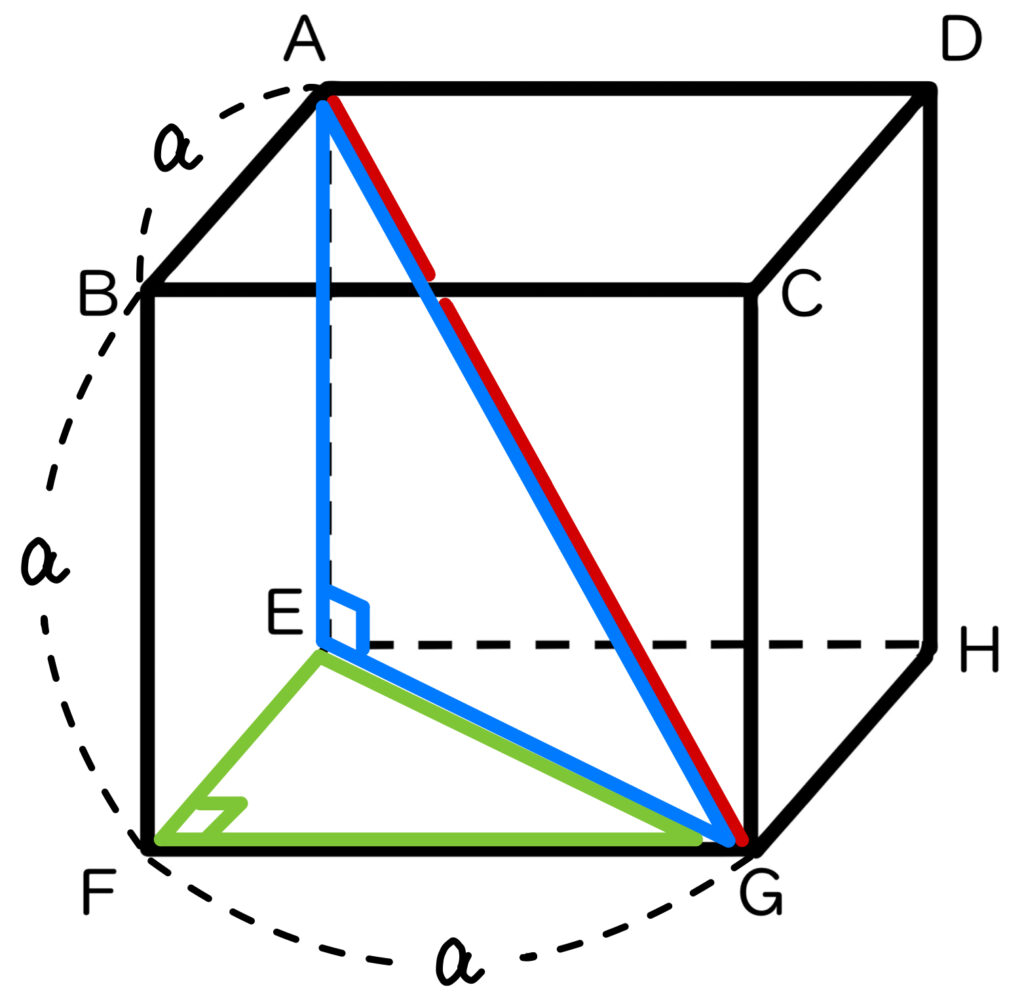
△\(EFG\) は直角三角形なので、三平方の定理より
\(EF^2 \,+ \,FG^2\,=\,EG^2\) が成り立ちます。
つまり
\(a^2 \,+ \,a^2\,=\,EG^2\)
よって
\(EG^2 \,=\,2a^2\) … ②

② を ① に代入して
\(a^2 \,+ \,2a^2\,=\,AG^2\)
\(AG^2 \,= \,3a^2\)
\(AG \,> \,0\) より
\(AG\,= \,\sqrt{3}\,a\)
となる。

このことから、立方体の対角線の長さは 1辺の長さに \(\sqrt{3}\) をかけるだけでいいことがわかりますね！

練習問題

下の図のような、1辺が \(5\,cm\)の立方体の対角線の長さを求めなさい。

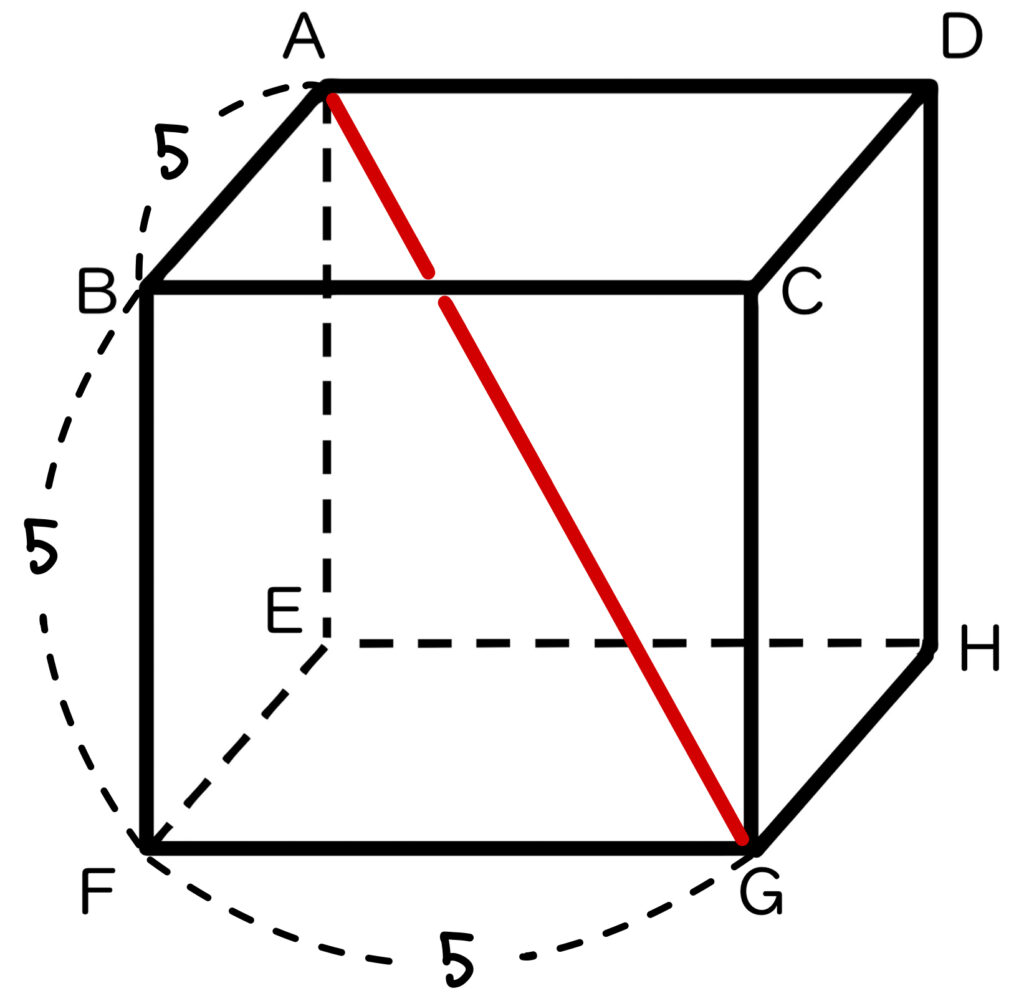
まとめ