中3で学習する展開。そもそも展開って?応用問題が難しくてできない!と思っている人もいるかと思います。
この記事では、展開について、その意味と具体的な応用問題問題を3パターンに分けて、その解き方を徹底解説します!
そもそも展開とは
展開とは、単項式や多項式の積の形の式を、かっこをはずして単項式の和の形に表すことをいいます。
具体的には
・\(2a(2a+3)=\)\(4a^2+6a\)
・\((x+2)(x+3) =\) \(x^2+5x+6\)
のように項だけの式の形にすることです。
因数分解の逆の操作ともいえますね。
応用問題1
次の式を展開しなさい。
\((x+y+z)^2\)
展開するときには
①単項式を分配法則によって、かっこの中の項にかける
②乗法公式を使う
\(\, \,\)⑴ \((x+a)(x+b)=x^2+(a+b)x+ab\)
\(\, \,\)⑵ \((x+a)^2=x^2+2ax+a^2\)
\(\, \,\)⑶ \((x-a)^2=x^2-2ax+a^2\)
\(\, \,\)⑷ \((x+a)(x-a)=x^2-a^2\)
の順で、展開できないか考えていきます。
今回の式では、どのように展開するのでしょうか?
問題の式の\(\,\) \(x+y=A\)\(\,\)と置き換えて考えると
②の乗法公式⑵が使えることがわかります。
\((x+y+z)^2\)
\(=(A+z)^2\)
\(=A^2+2zA+z^2\)
\(A\) を \(x+y\) に戻して
\((x+y)^2+2z(x+y)+z^2\)
\(=\)\(x^2+2xy+y^2+2xz+2yz+z^2\)
となります。
\(x^2+y^2+z^2+2xy+2yz+2zx\)
と並び替えると、オシャレです。(高校数学でよくこの式が出てきます。)
応用問題2
次の式を展開しなさい。
\((x+y+2)(x-y+2)\)
これも先ほどと同じように、同じ項のまとまりを置き換えたいところですが、\(x+y\) と \(x-y\) では同じ項のまとまりではないので、置き換えることができません。
ですが、( )の中の項の順番を入れ替えると
\((x+2+y)(x+2-y)\)
となり、\(x+2=A\)と置き換えて考えることができます。
\((A+y)(A-y)\)
\(=A^2-y^2\)
\(A\) を \(x+2\) に戻して
\((x+2)^2-y^2\)
\(=\)\(x^2+4x+4-y^2\)
となります。
応用問題3
次の式を展開しなさい。
\((x+y-1)(x-y+1)\)
これも先ほどと同じように、( )の中の項の順番を入れ替え、同じ項のまとまりを置き換えたいところですが、( )の中の項をどのように並べ替えても、同じ項のまとまりができません。
ですが、右のかっこ内の \(-y\) と \(+1\) が左のかっこ内の \(+y\) と \(-1\) とどちらも符号が違うことに注目し、\(-y\) と \(+1\) を \(-1\) でくくると
\( \{x+(y-1)\} \{x-(y-1)\}\)
となり、\(y-1=A\)と置き換えて考えることができます。
\((x+A)(x-A)\)
\(=x^2-A^2\)
\(A\) を \(y-1\) に戻して
\(x^2-(y-1)^2\)
\(=x^2-(y^2-2y+1)\)
\(=\)\(x^2-y^2+2y-1\)
となります。
どうしても解法が思い出せない場合
展開の応用問題において、解法が思い出せない場合は、一方のかっこ内の項をもう一方のかっこ内の項に分配すればよいです。(「総あたり」とよんでいます。)
【応用問題1】
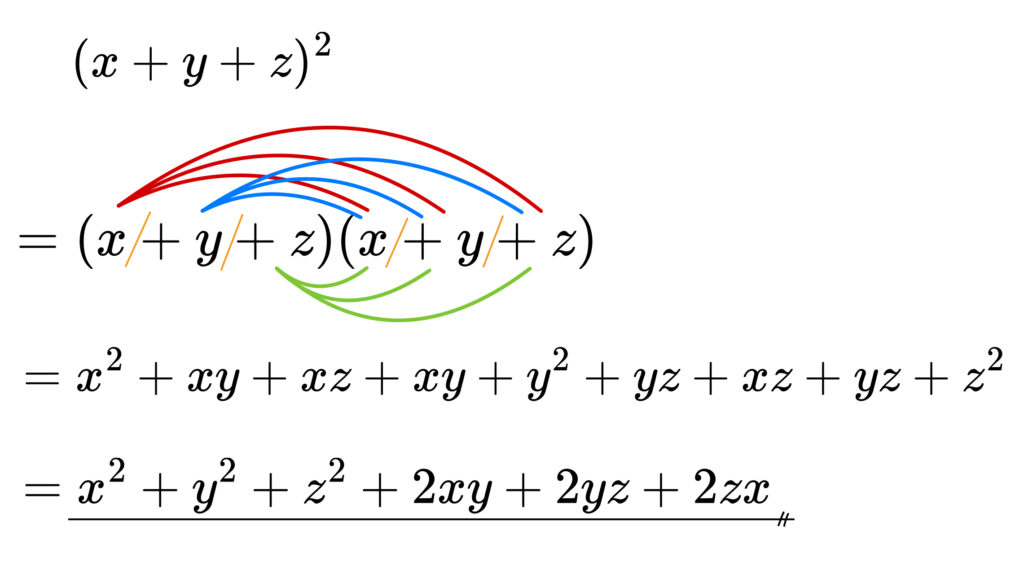
【応用問題2】
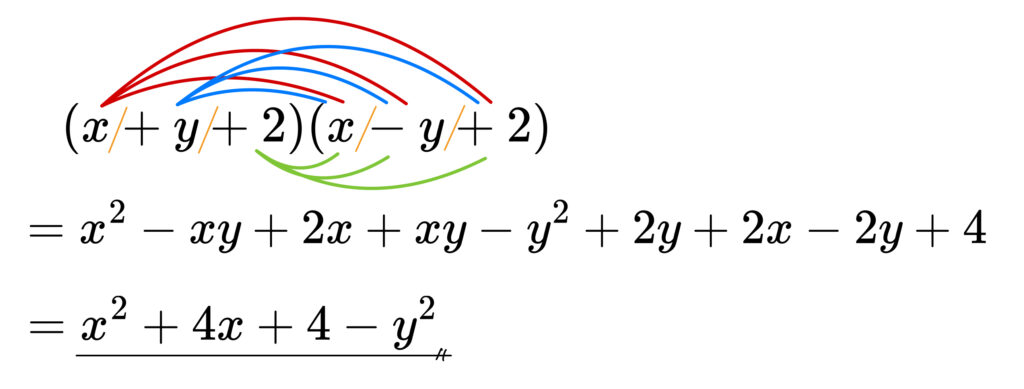
【応用問題3】
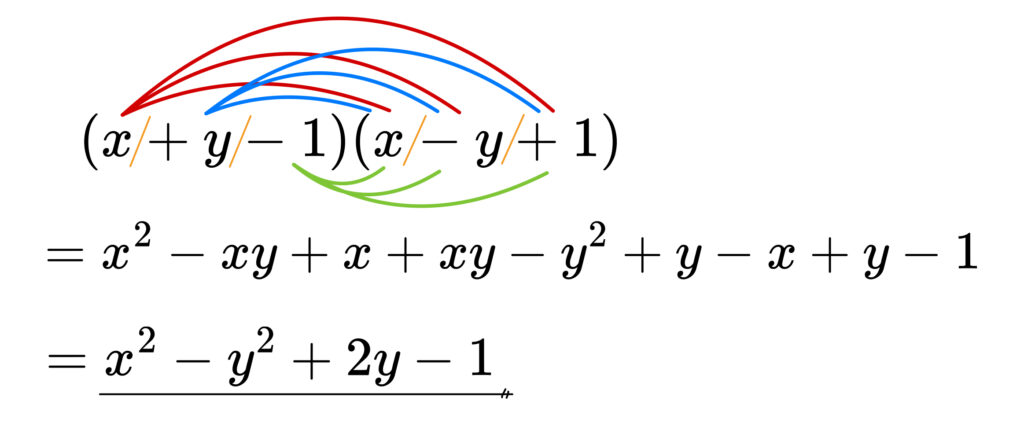
このように、「総あたり」なら、応用問題でもどんな問題でも答えを求めることができますので、絶対に諦めないでください!!
まとめ
展開の応用問題は
● かっこ内の項の順番を入れ替え、同じ項のまとまりを1つの文字に置き換えて、乗法公式を使って展開する。
● かっこ内の項の順番を入れ替えても同じ項のまとまりができなければ、符号が異なる項2つをを”−1″でくくり同じまとまりをつくる。
● 解法を忘れてしまったときは、総あたりで展開する!
このポイントがとても大切です!
にほんブログ村




コメント