通分とは何？どういう意味か図を使って解説！

分数の計算でよく出てくる 「通分」 という言葉。

「分母をそろえること」と習ったけど、なぜそんなことをするの？ と思ったことはありませんか？

この記事では、通分の意味や 「なぜ分母をそろえるのか？」 を図を使ってわかりやすく解説します！

通分とは？分母をそろえること！

通分とは、分数の分母をそろえること です。

たとえば、次のような分数があります。

\(\displaystyle \frac{1}{2}\) と \(\displaystyle \frac{1}{3}\)

これらの分数の 分母をそろえる と、こうなります。

\(\displaystyle \frac{1\color{red}{\times3}}{2\color{red}{\times3}}\) ＝ \(\displaystyle \frac{3}{6}\) と \(\displaystyle \frac{1\color{red}{\times2}}{3\color{red}{\times2}}\) ＝ \(\displaystyle \frac{2}{6}\)

このように 分母の最小公倍数を分母と分子にかけて、分母をそろえる操作を「通分」 といいます。

なぜ通分するのか？

では、なぜ通分が必要なのでしょうか？

それは、分母が違うと、足し算や引き算といった計算ができないから です！

ピザを使った例で考えてみる

たとえば、\(\displaystyle \frac{1}{2}\) と \(\displaystyle \frac{1}{3}\) のピザを足す ことを考えます。

• \(\displaystyle \frac{1}{2}\) は、ピザを 2 等分したうちの 1 枚

• \(\displaystyle \frac{1}{3}\) は、ピザを 3 等分したうちの 1 枚

この 2 枚のピザを足すと、何等分にした何枚分になるでしょう？

このままでは、足すことができませんよね。

そこで、それぞれのピザを 6 等分（分母をそろえる）して考えると…

\(\displaystyle \frac{1\color{red}{\times3}}{2\color{red}{\times3}}\) ＝ \(\displaystyle \frac{3}{6}\) （ 6 等分したうちの 3 枚）

\(\displaystyle \frac{1\color{red}{\times2}}{3\color{red}{\times2}}\) ＝ \(\displaystyle \frac{2}{6}\) （ 6 等分したうちの 2 枚）

これなら 分け方がそろっているので 足すことができます。

\(\displaystyle \frac{3}{6} + \displaystyle \frac{2}{6} = \displaystyle \frac{5}{6}\)
となります。

通分すると、分数の 「分け方」がそろうので、足し算や引き算といった計算ができる のです。

通分しても数の大きさは変わらない！

通分するときによく、

と考える人がいます。

しかし、通分は 見た目の数は変わりますが、元の分数と同じ大きさを表しています！

なぜなら、

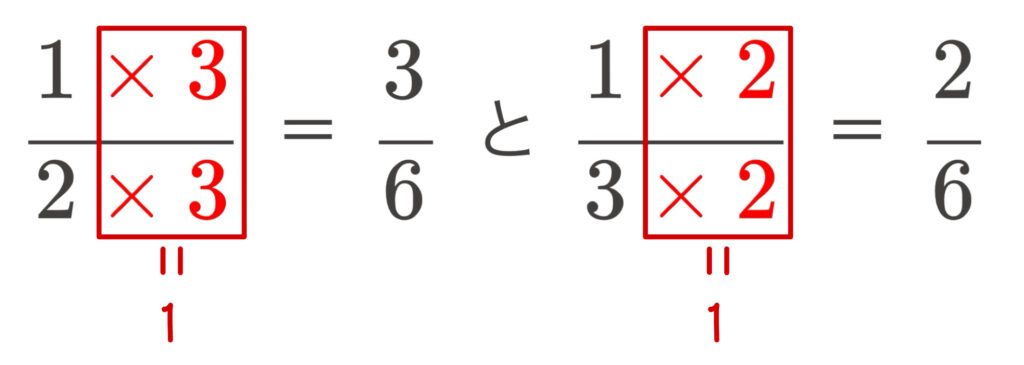
\(\displaystyle \frac{1}{2}\) を通分するときにかけている数は \(\displaystyle \frac{3}{3}\) 、つまり 「1」 をかけていることと同じなので、当然、数の大きさは変わりません！

\(\displaystyle \frac{1}{3}\) を通分するときにかけている数は \(\displaystyle \frac{2}{2}\) 、これも 「1」 をかけていることと同じなので、数の大きさは変わりませんね。

実際にピザの絵で見ても、\(\displaystyle \frac{1}{2}\) と \(\displaystyle \frac{3}{6}\) 、\(\displaystyle \frac{1}{3}\) と \(\displaystyle \frac{2}{6}\) はそれぞれ同じ面積を表していることがわかりますよね。

つまり、通分しても、数の大きさは変わらない ということです！

まとめ