最大公約数や最小公倍数を「約数や倍数を書き出して調べる」って正直めんどうだと思いませんか?
実は、素因数分解を使えば、もっと簡単に、確実に答えが出せるんです。
でもこの方法、教科書のすみっこにちょっと書いてあるだけで、授業ではあまり紹介されないことも。
今回は、素因数分解を使った最大公約数・最小公倍数の求め方を、例題を交えてわかりやすく紹介します!
そもそも素因数分解ってなに?
ある自然数を、「2」「3」「5」などの素数だけのかけ算で表すこと
たとえば、「42」は
\(42 = 2 \times 3 \times 7\)
のように表せます。
この素因数分解を使うと、最大公約数や最小公倍数を、簡単に、確実に求めることができるんです。
42と60の最大公約数・最小公倍数を求める
まずはそれぞれ素因数分解する
42と60をそれぞれ素因数分解すると
\(42 = 2 \times 3 \times 7\)
\(60 = 2 \times 2 \times 3 \times 5\)
となります。
最大公約数を求める
最大公約数は、共通する素因数をかければ求めることができます。
42と60では、2と3が共通する素因数なので、
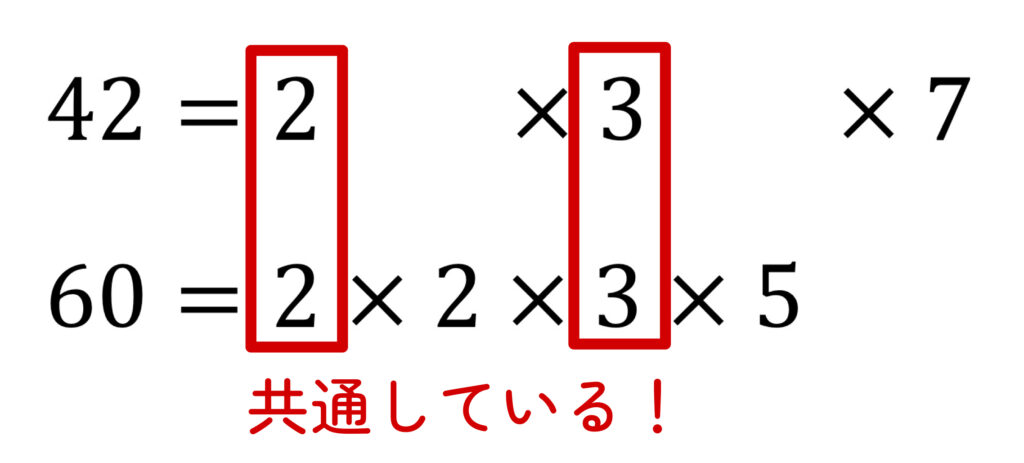
それらをかけて、最大公約数は
\(2 \times 3 = 6\)
となります。
どうしてこの方法で求められるのか
素因数分解したときの素因数は、どれも元の数の約数であることから、2つの数の最大公約数はそれぞれの素因数の共通しているのものをすべてかけ合わせればよいのです!
最小公倍数を求める
最小公倍数は、共通していない素因数を補うようにかければ求めることができます。
42と60では、42にとって2と5が共通していない素因数なので

42にそれらをかけて、最小公倍数は
\(42 \times 2 \times 5 = 420\)
となります。
もちろん、60にとっては7が共通していいない素因数なので
60に7をかけて、最小公倍数は
\(60 \times 7 = 420\)
と求めることもできます。
どうしてこの方法で求められるのか
倍数とは元の数を何倍かした数であり、どんな整数をかけても元の数の倍数にはなりますが、2つの数の最小の共通している倍数を見つけたいので、2つの数の共通していない素因数だけをかければよいのです!
書き出して求める方法の限界
たとえば、42の倍数をずらっと書き出してみると…
42、84、126、168、210、252、294、336、378、420、…
60の倍数は…
60、120、180、240、300、360、420、…
👉どちらにも出てくる最初の数が「420」ですが、ここにたどり着くのに倍数を何個も書かないといけないし、計算ミスをするリスクも。
素因数分解を使えば、書き出さずに正確な答えが出せるのです!
まとめ
● 素因数分解を使えば、最大公約数・最小公倍数を正確に速く求められる。
● 最大公約数は、共通する素因数をかける
● 最小公倍数は、共通していない素因数を補うようにかける
この方法を応用すれば、3つの数の最大公約数・最小公倍数も求めることができますよ!
にほんブログ村




コメント